CONCEPT
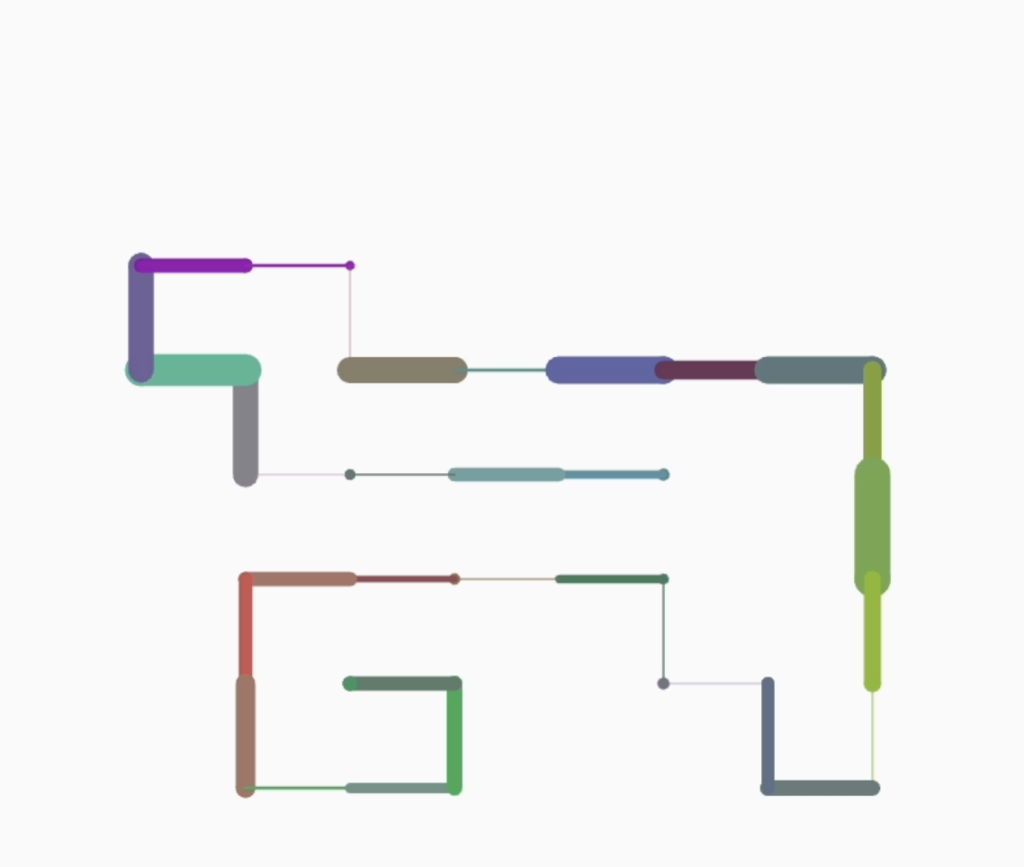
So, for this week’s coding assignment, I tried to implement the self-avoiding walk. I am a mathematics major too and I wanted to explore a mathematical concept through what we’ve been learning in class. In mathematics, a self-avoiding walk (SAW) is a sequence of moves on a lattice path that does not visit the same point more than once. To make it more interesting and look like a computer chip, or gaming area (of pac-man, say), or a network of pipelines, or points and paths on a map, I played around with the color() and strokeWeight() property of the lines and dots I was plotting. With someone randomness using noise as we learnt in class, I was able to achieve interesting and fascinating results!
EMBEDDED SKETCH
WORKING VIDEO
See my self-avoiding walk walking! 🙂
KEY TECHNICAL ASPECTS
There are 2 code snippets I would like to highlight:
1. First is the core concept of the self-avoiding walk – how it chooses which direction to go next and how it avoids itself. For this, I populated an array with available spaces for the walker to move on the basis of which vertices were already visited or not. And then, instead of randomly choosing from numbers between 1-4, the walker randomly chooses a place to go from this array of available spaces.
this.matrix = []; // holds position where all the walker has been --> initially populated to false, changed to true when walker visited that spot
// for populating the spaces available to walker
let options = []; // to store which options available to go to
if (this.isValid(this.x+1, this.y)) //i.e. right available space
options.push(0);
if (this.isValid(this.x-1, this.y)) //i.e. left available space
options.push(1);
if (this.isValid(this.x, this.y+1)) //i.e. up available space
options.push(2);
if (this.isValid(this.x, this.y-1)) //i.e. available space
options.push(3);
// for choosing where to go from the available spaces
let choice;
if (options.length > 0) {
choice = (random(options));
if (choice == 0)
this.x++; // go right
else if (choice == 1)
this.x--; // go left
else if (choice == 2)
this.y++; // go up
else if (choice == 3)
this.y--; // go down
this.matrix[this.x][this.y] = true; // mark this place as visited
}
else {
print("OVER");
// text("OVER", width/2 - 10, height/2);
noLoop();
}
isValid(i, j) { // checks if this matrix space / vertex is available to visit or not
if (i < 0 || j < 0 || i >= num_rows || j >= num_cols)
return false;
return (!this.matrix[i][j]);
2. The second thing I want to highlight is my code for random colours and dot sizes.
// for randomizing dot size based on random gaussian
let w = randomGaussian(5,3);
strokeWeight(w);
// for randomizing stroke color based on noise
let n1 = noise(t);
let n2 = noise(t+50);
let n3 = noise(t+100);
t += 0.5;
let c1 = map(n1, 0, 1, 0, 255);
let c2 = map(n2, 0, 1, 0, 255);
let c3 = map(n3, 0, 1, 0, 255);
let c = color(c1,255-c2,c3)
//plot the point / dot
stroke(c);
point(this.x * this.step + this.step/2, this.y * this.step + this.step/2);
// plot the line
strokeWeight(1);
line(this.prev_x * this.step + this.step/2, this.prev_y * this.step + this.step/2, this.x * this.step + this.step/2, this.y * this.step + this.step/2);
IMAGE GALLERY
Some more drawings that occurred in the process:

FURTHER DEVELOPMENTS
Currently, the self-avoiding walk gets stuck once it reaches a point and has no more places to go. It has travelled to all its neighbouring points and since it is self-avoiding, it can’t cross itself again. This is what we call a ‘dumb’ self-avoiding walk, which just randomly chooses a point to move to next without thinking about the future – whether this will lead me to continue on a longer path or this move will get me stuck. Hence, the next step would be to implement a ‘smart’ self-avoiding walk, which can keep track of whenever it gets stuck and go back and choose a better move which will allow it to continue for longer. The algorithm for this is rather complicated as it requires backtracking and dynamic programming, but still doable and somewhat similar to the computer algorithms for solving mazes.
COMPLETE CODE
https://editor.p5js.org/shreyagoel81601/sketches/0ooUuQdcW
