Author: Ahmad Hafizh

Anthropocene Tornadoes

Anthropocene: a thought that humans have become a geological force. -Vladimir Verdansky

Climate change is happening, and it will reshape the way we think about our daily lives. At the epicenter of this global phenomenon is us: humans. Throughout the ages, we have been kneeling under the force of nature. But beginning in the Industrial Revolution and onwards, we began to revolutionize how we do things. Without looking at its long-term consequences, we conquered nature and became a destructive force in return.

Anthropocene Tornadoes is my attempt and initiative to raise awareness regarding this matter. It is a simple program but a philosophical piece that combines interactiveness and mindfulness.

The goal is simple: You are the tornado. Destroy.

Sketch DemoInspiration and Challenges

As some of you might have seen from the previous drafts, my initial concept of this project was to use AR systems to generate the tornado and have the user play around with it. But, after really really arduous long hours of testing and developing, I concluded: that AR is too limited and not the best environment to do this project.

I spent a good 5-6 hours trying to solve the big issue of interactiveness. I wanted the user to experience something different than the usual things displayed in the IM Show. But it seems like for this case, using AR was not the key.

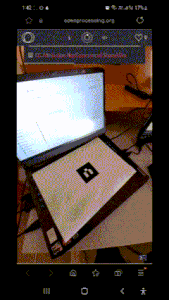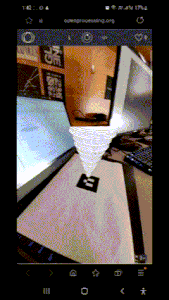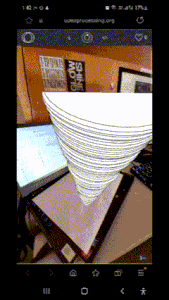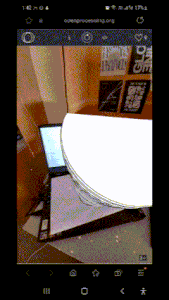
SimpleAR library has a solid limitation: the ENTIRE p5.js sketch will turn into a camera. The camera then scans a marker, which then displays the sketch in the draw() function. But, because of this, it also significantly limits the amount of choice I have over the interaction the user can make. Plus, using camera and rendering particles were way too heavy for the intended viewing device, smartphones and ipads.

But the original concept remains the same. The program is a somewhat tornado simulation. It begins with a vortex-shaped particles that speeds up and inflates once the user move and ‘eat’ buildings represented by the rectangle.

The project’s visual choice is inspired by old 3d modeling software capabilities. Simple, abstracted, low-poly shapes are joined together to hopefully take the shape of something. In Anthropocene Tornadoes’ case, it was a city filled with skyscrapers, a grassland, and a tornado.

How The Program Works

▶️The sketch runs on a WebGL-based rendering, meaning that is has 3D capabilities. To adjust the camera, I used a p5.js library called EasyCam, which allowed me to manipulate the camera and only allowed the user to zoom in-and-out without rotating the canvas.

▶️The core of the program, the tornado, works by having a Particle class generated in a vortex-like shape in the beginning. This class is a vector class. It starts with a circle which converges downwards. This gives the effect of the vortex.

When the tornado collides with a skyscraper, it will increment a speed modifier, speedMultiplier, that effects the radius of the circle. Thus, with each particle spinning on this radius, it gets bigger and bigger. Combine it with noise, lerp, constrain, and you get yourself a somewhat convincing tornado-like particle system.

update(speedMultiplier) {
    // Increment the angular position to simulate swirling
    this.angle += (0.02 + noise(this.noiseOffset) * 0.02) * speedMultiplier;

    // Update the radius slightly with Perlin noise for organic motion
    this.radius += noise(this.noiseOffset) * 5 - 2.5;

    // Constrain the radius to a certain bound
    this.radius = constrain(this.radius, 20, 500);

    // Update height with sinusoidal oscillation (independent of speedMultiplier)
    this.pos.y += sin(frameCount * 0.01) * 0.5;

    // Wrap height to loop the tornado
    if (this.pos.y > 300) {
      this.pos.y = 0;
      this.radius = map(this.pos.y, 0, 300, 100, 10); // Reset radius
    }

    // Update the x and z coordinates based on the angle and radius
    this.pos.x = this.radius * cos(this.angle);
    this.pos.z = this.radius * sin(this.angle);

    this.noiseOffset += 0.01 * speedMultiplier;
  }

▶️The collisions are handled by a collision check, which also plays collision sounds. It works by splicing the collided skyscraper stored in the skyscraper array.

for (let i = skyscrapers.length - 1; i >= 0; i--) {
    let skyscraper = skyscrapers[i];
    let distance = dist(tornadoX, 0, tornadoZ, skyscraper.x, 0, skyscraper.z);

    // If tornado is within a threshold distance, remove the skyscraper
    if (distance < 50) {
      skyscrapers.splice(i, 1);
      fill(0, 100, 100);
      speedMultiplier += speedIncrement;
      let randomCollisionSound = random(collisionSounds);
      randomCollisionSound.play();
      continue;
    } else {
      fill(0, 0, 100);
    }

▶️The rest of the program is handled by a programStateLogic function which controls the state of the program and its appropriate ending.

Interaction

The program, as mentioned earlier is intentionally a simple one. The user moves the tornado using the mouse which controls the vector location of the tornado.

ENDINGs: There are three possible endings within the program.

1️⃣The user consumed all buildings.

2️⃣The user ‘failed’ to consume all buildings within the respective time

3️⃣The user does not decide to do anything and becomes a ‘savior’

These endings were created for the users to reflect our own actions as a human, and how we became a destructive force of nature. Nature here, being the tornado that we control.

User Testing & Reactions

Because my body said that it’s time to get sick at the end of the semester, I could not almost finish this project in time. But, I was able to receive feedback and user testing albeit from far away.

I sent the sketch link to some of my friends and asked them a simple question: How long did it take for you to figure out how to move the tornado?

I found two issues: a) While it is true that the user got the hang of it, I wanted the interaction to be more clear, so I added a simple mouse move command in the center of the screen. (Let’s not give super clear instructions shall we?)

b) The white screen. On some devices, the ending screen did not render the text properly. I fixed this and gave a clear message on what the ending is and what to do if the user wants to redo the program.

IM SHOWCASE

For the IM Showcase, I think it was very interesting to see how people reacted to both our midterm and final project. The leap from two-dimensional program to a three-dimensional is a huge one. From the ‘gameplay’, I believe that the endings could have been made more clear on how to obtain them. But regardless, it was interesting to give people a bit of information regarding tornadoes!

Reflections and Future Improvements

I wanted to work on the visuality of the project. Had I not been hospitalized for a few days during the holiday, I might have had more time to work on this aspect. But, after spending way too much time on the AR aspect and giving it up, I had no energy left to work on the visual aspect.

The project also surprisingly worked on mobile devices, although severely unoptimized. The gesture controls do work, but they don’t work very well. I was also thinking of doing something regarding the EF Scale. Perhaps, depending on how big the tornado gets, a color or something else changes. Also, for some reason the tornado flies upwards even though I did not change anything in that coordinate? what?

Regardless, this project was really fun for me to work on (although stressful at times). It really taught me how to emulate physics, but also how demanding simulating it for the machine.

Resources Used

touches – a p5.js feature I did not use

Tornado Sound #1 | Sound FX – YouTube – tornado sound

collision sounds – from plater addon, curseforge

p5.js WebGL camera – Daniel Shiffman

Tornado simulation inspiration – emmetdj

ChatGPT for the amazing debugging.

 

Concept

I want to make a tornado. A tornado is a violently rotating air column extending from a thunderstorm to the ground. A dark, greenish sky often portends it. Black storm clouds gather. Baseball-size hail may fall. A funnel suddenly appears, as though descending from a cloud. The funnel hits the ground and roars forward with a sound like that of a freight train approaching. The tornado tears up everything in its path [National Geographic].

Show Plan

Assuming that we are going to use traditional tables, I  wanted the final presentation to be like a science fair thing. The carton will hold all information regarding tornadoes, mitigation, and things everyone needs to know about it. In this case, I’ll use a carton and fit information inside (paper cut-out, etc.) and then have my p5.js there to be ‘scannable’.

My main attraction would be to use AR technologies. Yes, having users scan a QR code, would attract them (mwahaha).

Technicality

I am using a p5.js plugin called simpleAR, which allows the digital sketch to be projected into a ‘marker’. This plugin was made by Tetunori. And given this medium, I wanted to push, nudge, and slap myself a bit harder this time by working on a three-dimensional workspace using WebGL.

The tornado is made out of particle systems with a custom force that simulates vortex. My plan for the interaction is simple: as the user swipes the tornado, it spins faster and creates a bigger, faster, scarier tornado.

Prototypes

Philosophy, Why, and Passion

Humans have always feared nature. Powerless against its judgment against our kind. But beginning after the Industrial Revolution, we became a force more destructive than nature itself–we are the Anthropocene.

Milton, Sharjah, Sumedang, and other places around the globe. As an effort to spread awareness regarding climate change, I created this final project. I am not a policymaker, nor an environmental expert. But if there is anything I can do to help our home, this is the least I could do.

Challenges I Found (so far!)

📸As you might have noticed from the prototype demo, I am displaying my canvas without any background. During the experiment, I found out that recent releases of the p5.js editor handle transparency in WebGL like water and oil-they don’t go well together. Using the clear() method, the behavior expected was to have no background. Instead, it did give a solid black background.

I spent meticulous hours trying to piece things together as to why the transparency did not work until I stumbled upon a forum question.  Because by native the editor does not support transparent background anymore, I decided to switch my work to OpenProcessing since they handle WebGL differently, and most importantly, the clear() method works as intended.

🤌Design and Interactivity. I am conflicted on what to decide here: Should I make a ‘stylized’ tornado that does not follow its natural laws, or should I create a scaled simulation? How much does my interactivity count as ‘interactive’?

There are certain limitations within the AR library I am using. Particularly, there is no handshake between the screen and the canvas. What I mean by this is that my original plan was to use gestures as a way to interact with the tornado. But to do this is very hard because there is no communication between the screen touch and the canvas. So either I have to resort to buttons (which is meh) or do something else entirely.

1) Stylized 3d tornado

2) PARTICle system tornado

---

DRAFT PROGRESS

After some thought and thinking, I finally decided to use the particle system tornado as the default base. For now, I added two new features:

 

a) Skyscrapers: Rectangles of various heights are now scattered across a plane. These skyscrapers have ‘hitbox’ that reacts to the tornado.

b) Tornado-skyscraper collision check: When the tornado collides with a rectangle, it will ‘consume’ them and increase the particle speed. To implement this feature, I introduced speedmultiplier variable.

update(speedMultiplier) {
    // Increment the angular position to simulate swirling
    this.angle += (0.02 + noise(this.noiseOffset) * 0.02) * speedMultiplier;

    // Update the radius slightly with Perlin noise for organic motion
    this.radius += map(noise(this.noiseOffset), 0, 1, -1, 1) * speedMultiplier;

    // Update height with sinusoidal oscillation (independent of speedMultiplier)
    this.pos.y += sin(frameCount * 0.01) * 0.5;

    // Wrap height to loop the tornado
    if (this.pos.y > 300) {
      this.pos.y = 0;
      this.radius = map(this.pos.y, 0, 300, 100, 10); // Reset radius
    }

    // Update the x and z coordinates based on the angle and radius
    this.pos.x = this.radius * cos(this.angle);
    this.pos.z = this.radius * sin(this.angle);

    this.noiseOffset += 0.01 * speedMultiplier;
  }

What is left:

▶️Visuality: Improve the visual aspects of the sketch

▶️AR Port: Port the features into AR and move the tornado based on the device’s motion.

🛠️Fix the tornado going upwards whenever it reaches a certain speed. Mostly due to the speed multiplier and particle reacting together.

Resources Used

Stylized Tornado – Aexoa_Uen

Tornado Simulation – Emmetdj

EasyCam – James Dunn

Sharjah Tornado

Sumedang, Indonesia Tornado 

CONCEPT

I explored cellular automata quite a bit, looking at its one-dimensional and two-dimensional aspects.  A particular idea came to my mind: What if I create an ocean comprised of grid cells and ripples by mouse press? The result is Cellular Islands.

SKETCH

HOW IT WORKS

Cellular Islands uses two-dimensional cell interactions. The canvas is built on top of grids. These grids then store two values: 0, and 1. Both values are then placed on current and previous states.

The rules of cells are as follows:

1) Each cell state is the average update of its neighbor and previous state
2) Two grids: Current holds current wave height; Previous holds wave from past time
3) When the mouse is pressed, a wave is generated and follows the wave equation.

The wave equation stores a ‘height’ value for each cells affected by the mouse as the epicenter. These values determine the brightness of the cells, mimicking the waves as well.

CHALLENGES

Getting the waves to not look absolutely horrendous was quite difficult. I then figured that by adding a dampening to the force, it would result in a more natural movements.

AOI (AREAS OF IMPROVEMENT)

💡I think visualization and adding more colors would be nice. But because I imagined in the beginning that this would be a simple 0s and 1s program, it is black and white.

Resources Used:

Water Ripple Tutorial – Daniel Shiffman

Look here hehe

Concept

Initially, I wanted to make a simple tower defense game where players have to block the oncoming flocks of enemies. However, the execution was more difficult than I intended. My next idea then came from the behavior of birds themselves.

birds in a flock pay close attention to the birds around them—particularly their closest neighbors.

But they might collide with birds from other species or different groups. Hence, my concept becomes as so: What if I make a flock of two or more different bird groups? A) They must group up with the same group B) Avoid different group.

Sketch Prototype

Here, what I did was to represent the boids in two colors by introducing a color property. This then allows me to modify the other behaviors and forces such that they interact with this color property. Particularly, the separation, alignment, and cohesion are affected by this change.

let emoji = this.color === "#C96868" ? "" : "";

separate(boids) {
  let desiredSeparation = 25;
  let steer = createVector(0, 0);
  let count = 0;
  for (let i = 0; i < boids.length; i++) {
    let other = boids[i];
    let d = p5.Vector.dist(this.position, other.position);
    if (d > 0 && d < desiredSeparation && other.color === this.color) {
      // Only same color
      let diff = p5.Vector.sub(this.position, other.position);
      diff.normalize();
      diff.div(d);
      steer.add(diff);
      count++;
    }
  }

But what if, and what happens when we connect a string between each boids? What visuals would it look like, and how would it behave?

I followed this intuition and attempted to add strings that attach to each boid. Of course, they are also vector which means these strings are attracted and affected by external forces.

//Connect
  //Function to connect a string between each boids
  connect(boids) {
    for (let other of boids) {
      let d = p5.Vector.dist(this.position, other.position);
      let maxDistance = 200; // Maximum distance for drawing a line

      // Only draw line if within maxDistance and the other boid is not itself
      if (d > 0 && d < maxDistance) {
        stroke(200, 50);
        strokeWeight(0.5); 
        line(
          this.position.x,
          this.position.y,
          other.position.x,
          other.position.y
        );
      }
    }

Alas, then it suddenly happened. But what a minute–what is this?

Aha! I have just visualized the connection between each boids. Instead of drawing lines on the current information, these lines draw from previous (a frame delay) information of the boids. In essence, they are the boids, birds, and flocks themselves, but represented in lines instead! It seems that the lines are following particularly the white boid but acts just like both red and white boid. I am unsure why.

Challenges & Improvements

➡️During the red-white test, I wanted the boids to return towards the screen again whenever it touches the edge of the canvas. I tried many implementations but found that by multiplying it to -1, or the negative vector does the job best.

➡️For the color checking between each boid, initially I used an if statement. While it worked, I also learned that ternary conditional statement worked better for this implementation where it just pairs up the color code and emoji.

🛠️Performance is quite an issue right now because the sketch is doing three calculations: One red, one white, and for the strings. In the future, I hope to bring more optimizations especially lifetimes for each vector to make sure that they don’t hog the machine.

Resources

All about birds – Cornellab

Ternary Operators – JavaScript

Inspiration & Concept

For this assignment, I just created a wandering UFO that abducts people if they get too close to the UFO. That’s it.

Sketch

How it Works

I just used the wander and persuade methods, where the UFO uses wander as a default state. Whenever it is close to a target, it will switch to persuade method.

Improvements

Add a city map, sounds, and make a game out of it — profit.

Unnatural Coolors

Unnatural Coolors is a p5.js project that simulates a select few parametric equations hand-picked by the author, (me). This project uses a p5.js vector framework to plot the equations. In addition to the standard mathematical plotting, Unnature Coolors also simulate how wind, and Perlin noise, affect the whole drawing. Essentially, a slight change, inevitably, creates a significantly different outcome. Mimicking the common occurrences of randomness in nature.

The smallest decision in life can at times, lead to the biggest outcome.

Concepts & Inspiration

I have always been fascinated by the unique patterns that appear in mathematical models, which often also occur as part of nature itself. As I scoured the internet and math textbooks alike, I found parametric equations to emit its own beauty. Instead of defining x over y in a cartesian coordinate, parametric equations define x and y as functions of a third parameter, t (time). They help us find the path, direction, and position of an object at any given time. This also means, the equations work in any dimensions!

As I explored the internet for inspiration, I came across a Swiss artist, Ilhan Zulji, who studied randomness and implemented it into his work, creating a unique generative art style that reminds me of an ‘ordered chaos’. His work consists of creating shapes, and patterns, that are based on mathematical models, adding randomness into it, while maintaining some kind of structure and balance to make the visual appealing. Including the interactive elements, which allow the user to control the randomness to a certain degree, adds another layer of immersiveness to the viewing experience.

How Unnatural Coolors Works

The Particle class is responsible for the creation of particles drawn on the sketch. It takes the predetermined equation and translates it into the x-position, and y-position of the particles. To achieve a smooth motion, I put some offset between each particle. The particles are also affected by external forces from noise and wind, which makes them more dynamic. Then, between the distance of two particles, I formed a stroke of lines.

class Particle {
  constructor(timeOffset, xEquation, yEquation, lifetime) {
    this.timeOffset = timeOffset;
    this.prevPos = null;
    this.xEquation = xEquation;
    this.yEquation = yEquation;
    this.lifetime = lifetime; // Lifetime in frames
    this.maxLifetime = lifetime; // Store the original max lifetime
  }

Colors are produced by manipulating HSB color values. Originally, I wanted the colors to be a smooth gradient changing between one and another. However, after some testing, I decided that random colors between each particle were nicer.

display() {
    if (this.lifetime <= 0) return; // Skip rendering if lifetime is over
    
    // Calculate alpha based on remaining lifetime
    let alphaValue = map(this.lifetime, 0, this.maxLifetime, 0, 255); // Fade from 255 to 0
    //let hueValue = map(t, -6, 6, 0, 360); // Changing color over time
    let hueValue = random(0, 360) 
    stroke(hueValue, 100, 100, alphaValue); // HSB color with fading alpha

External forces, such as the wind and noise, are pre-calculated and initialized beforehand. These values are set by the slider below the canvas. This is done to ensure that the drawings start from the determined positions when the canvas starts or is refreshed.

// Wind slider with only 3 states (1 = left, 2 = no wind, 3 = right)
windSlider = createSlider(1, 3, 2);
windSlider.position(10, canvasBottom + 80);

noiseSlider = createSlider(0, 1, 0, 0.1);
noiseSlider.position(10, canvasBottom + 110);

let windLabel = createDiv('Wind');
windLabel.position(160, canvasBottom + 78);

let noiseLabel = createDiv('Noise');
noiseLabel.position(160, canvasBottom + 108);

initParticles();

Beyond Digital

Every artist dreams of having their work come to life. Unnatural Coolors was able to be brought to life by using the pen plotter. Below is a timelapse of the whole process of converting and drawing the best shape.

Challenges & Improvements

Most of the equations that I used are all in a single quadrant. Initially, I was confused as to why p5.js does not want to rotate the way I wanted it to be. To make sure that it forms the shape I desired, translate() was used three times, rotating 90 degrees each time.

In the beginning, I played around with fading the background a lot. By fading the background, I could ‘animate’ the motions of the shape plotting. However, after implementing multiple offset particles, it became apparent that this idea was no longer working. To combat this, I removed the background refresh, and let the canvas draw over instead.

I would love to see how this art can be generated using equations on the fly for future improvements. What I mean by this is that instead of predetermined equations, I want the users to tweak a certain equation, write their own, and plot unique shapes.

Check out the sketch here!

Useful Resources

# Drawing Parametric Equations – Umit Sen 

# Drawing Flow Fields with Vectors – Colorful Coding

# Quadio – Ikko. graphics 

# Audio Reactive Visuals – Leksha Yankov

# Audio Reactive Visuals CS Project – Austin Zhang

The Concept I am Aiming For

For the midterm, I have two ideas that I wanted to try and make. My first idea is that I would create:

a flowfield representation of mathematical parametric equations, with the mouse or any spawned external objects as an attractor to each field particle. 

Essentially (hopefully), is that the flowfields would be attracted forming, and shaping, a parametric equation on the left. And since different equations can form different fields, it would create variation in the art. I could also create a modifier for the equation so that it’s slightly different. This field can be interrupted and played around with an attractor vertex that is attached to the mouse. I am interested to see how this would work out.

Scouring the vast internet, I found an artist, Ilhan Zulji, who played around a lot with p5.js an interactive elements. My second idea would be to create:

Create waves, squares, ellipses, or any predefined shapes that react to external sources: audio, microphone, or camera, to form a new shape. 

Both of the examples I have shown above were from Zulji and Yankov, where they, through some equations and visuals, generated the art via parameters that respond to sound, acoustics, or noises. I want to see whether I could re-create this with my own personal touch.

---

Update #01 September 2024

After many thoughts and considerations, plus looking at the capabilities of the pen plotter, I decided to go with the first idea. The sketch below is what I have played around so far:

Essentially, I have particles that follow a certain mathematical equation. This movement is then disrupted by noise and wind (for now). For my final product, I wanted to add a fading feature, as well as more equations, and see how two equations can be combined so that it returns a new shape.

Potential Useful Resources

# Drawing Parametric Equations – Umit Sen 

# Drawing Flow Fields with Vectors – Colorful Coding

# Quadio – Ikko. graphics 

# Audio Reactive Visuals – Leksha Yankov

# Audio Reactive Visuals CS Project – Austin Zhang

Concept

While scouring through the internet looking for harmonic motions, I stumbled upon a mathematical figure called the Lissajous Figures.  Essentially, we put a grid table of circles of both the x and y axes. Then, if we unite the value of just one axis of one dot on the top and the value of the other axis of a dot on the side, you’ll get the coordinates of the dot where the rows intersect. And since they are moving at different speeds they make shapes. This phenomenon was studied cohesively by mathematician Jules-Antoine Lissajous in 1857 (Wolfram).

The most basic use of Lissajous figures is as the phase-space plots of harmonic motion in multiple dimensions. In other words, we can observe the speed-location graphs of repeating motion in 2D, 3D and beyond by using this graph.

Sketch

Development & How it works

Initially, I followed Shiffman’s tutorial regarding this particular harmonic motion. However, after giving it some thought, I wanted to experiment with it further. Instead of having a line drawing the shapes, what if I used multiple ellipses connected by lines, to expand beyond the initial shapes?  To do that, I had to simplify the code from arrays into singular objects.

for (let i = 0; i < pointNum; i++) {
    // Added phase to smooth out things 
    var phase = i * TWO_PI / pointNum;

    // Calculating the x and y positions
    var x = 160 * sin(a * t * phase + PI / 2);
    var y = 160 * sin(b * t * phase);

By utilizing for loops and the mathematical formula of LIssajous’ pattern, I was able to get somewhat a series of ellipses drawing just like the pattern. However, it was not close enough to the smooth, harmonic-like motion that I was aiming for.

Next, I added a trail lines between each ellipses by storing the information of each lines in a trails array. Combined with an added RGB color based off the x and the y positions, we get something like the sketch above.

// Store the trail information
    var trail = {
      x: width / 2 + x,
      y: height / 2 + y,
      r: r,
      g: g,
      bColor: bColor,
      alpha: 255
    };

    trails.push(trail);

Challenges Faced & Future Improvements

One particular challenge that I faced was making the motion smoother. After a bit of messing around with fading background and what nots, I discovered that by adjusting the time increment (t +=) to a very little amount, we can essentially, slice down into the tiniest fraction of frames, which results in a super smooth motion that I envisioned.

Playing around with the alpha values of the lines also somewhat affected the entire ellipses and canvas too, which results in a visual that I wanted to avoid very much. For future improvements, I wanted to see how the figures could be affected by other waves, such that they resemble something else, while oscillating back into its original forms. Perhaps even accompany it with acoustics to make it more appealing.

Resources Used

Lissajous Table in Processing – Daniel Shiffman

About Lissajous Curve – Wolfram

Lissajous Curve Discussions – Reddit

Reading Lissajous – Flemming, J., and A. Hornes.

Check out the sketch here!

Concept & Inspiration

This weekend, a lot of things happened. Because some unfortunate things happened, I decided to re-watch a few Marvel movies. After this I got an inspiration for Week 3’s assignment to create an eye that looks like Dormamu’s, the main antagonist of Doctor Strange.

Sketch

How it works

A particle class called Particle takes a few arguments (position, velocity, color). Overall, the class defines the behavior of a particle in the sketch. It contains a display() method that checks whether the particle is in a certain position, within a certain distance from the attractor, and whether it should be reflected or not. The particle’s path is visualized as a line between its current and previous positions.

class Particle {
  constructor(pos, v, color) {
    this.pos = pos; //Current Position
    this.pos_before = pos; //Previous Position
    this.v = v; //Velocity
    this.a = createVector(0, 0); //Acceleration, starting at 0,0
    this.color = color; //Color
  }
display() {
push();
stroke(this.color.x, this.color.y, this.color.z); //Stroke color based on XYZ
line(this.pos.x, this.pos.y, this.pos_before.x, this.pos_before.y); //Line from current to prev. pos this gives a trail effect.
pop();

If a particle comes into contact with an attractor (the one in the middle), a reflection occurs:

1. The particle is moved to the surface of the attractor by adjusting its position vector.
2. The velocity vector is  (multiplied by -1), and the particle is slightly rotated to simulate a reflection angle.
3. The velocity is also scaled down by multiplying 0.9 to simulate some loss of energy upon reflection.

The main sketch sets up the canvas, initializes particles, and controls their movement under the influence of gravity and collision dynamics. A central attractor is created as a rotating ring of gravitational points. Particles are randomly spawned outside the central attractor and move according to gravitational forces. Each particle reacts to the gravitational field by accelerating toward attractor points, and each particle can reflect off the surfaces of attractors if they collide.

Challenges and things to improve

I wanted to create a particle simulation that does not rely on particle systems. As an alternative, I relied mostly on arrays. Due to this, some calculations required me to deep dive into a bit of mathematics more than I initially planned. Also, initially, I wanted to make two eyes, but having two attractors provided to break the entire simulation, perhaps part of n-body problem characteristics. Thus, I did not want to go further into that concept.

Resources Used

Mutual Attraction – Daniel Shiffman

Inverse Square Law – Derek Owens

angleBetween – p5.js

rotate – p5.js

Visit the sketch here!

Concept and Inspiration

In the second week, we tapped into the world of vectors. I wanted to make something simple that requires speed, velocity, and everything around us with such aspects. Our class starts with bouncing a ball, and I revisited this concept again this time by applying vectors. What I wanted to recreate is a ball object falling into the water and creating this ripple-like effect.

Sketch

How it works

Using vectors, we can have p5.js calculate the speed of the object. The concept of ‘gravity’ here can be attributed to the y-position of the ball. Each time the ball bounces, its y-position should be decreased by cutting it in half. For the bounce to feel smoother, we introduce a bounciness variable that multiplies with the y-position negatively.

// bounce by multiplying the speed by the bounciness
  if (position.y + diameter / 2 > height) {
    position.y = height - diameter / 2;
    speed.y *= -bounciness;
    speed.x *= bounciness;
  }

Challenges faced

The tutorial that I followed only introduced the concept of ‘gravity’ in scalar methods. Extracting this information, I transformed the modes from scalar to vector. It was quite interesting, and quite the challenge!

As I originally mentioned, I wanted to make the ball form ripples when touching a certain height. While creating the ripples itself is a simple task using for-loops, making sure that it stays without being refreshed by the background is a challenge that I still haven’t overcome yet.

I have been trying to implement a few things, but I do not want my code to become overcomplicated. While I still have the time, I’ll try some stuff up to see if fixing this is possible.

Edit: I finally fixed the ripple problem, check it out here.

Resources Used

Bouncing Ball Simulation – Jeff Thompson