Author: Lukrecija Paulikaite

Concept:

For my midterm project I want to create an artificial particle life simulation. I want to create a system that functions on its own, has different components that interact and react to each other, kind of like in a cell. Each category of particles would have different features and functions within the system. I would attempt to make it appear as organic and as “alive” as possible. I want to design the artificial life based on some rules, however, I would prefer to prioritize aesthetics and the feeling that the system portrays in my design. Here is the inspiration:

Code:

For the code, I want to utilize the different functions inside the mover class to create the different particle groups. The sketch illustrates what I am starting with.  I will want to assign different behaviors (such as breathing of the bigger particles) and movement to different categories. I am also using the different forces we learned to make the movement more natural.

Complex parts:

The more challenging parts will be the different behaviours. For instance, I want to simulate emergence and create grouping behavior between the small particles. I would also like to explore the idea of creating some kind of structure from those groups and simulate an organism that develops new behaviors.

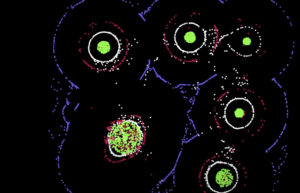
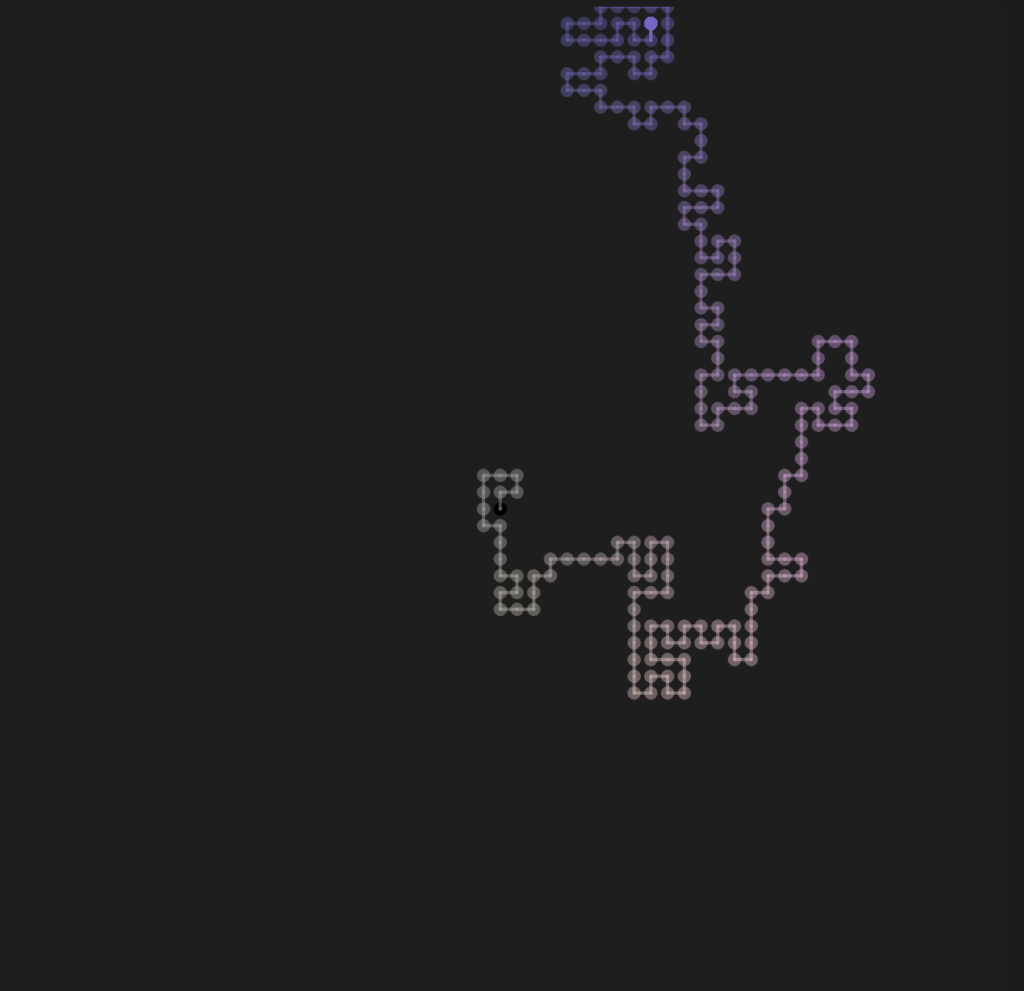For this assignment, I aimed to create an animated visual pattern using ellipses that oscillate back and forth in a circular motion. The key concept behind this project is the use of trigonometric functions (sine and cosine) to control the position and size of the ellipses over time. Additionally, the animation changes direction resulting in a dynamic visual effect. Since the goal of the assignment was to create a harmonic motion, my inspiration or the starting point was the sine and cosine functions in itself rather than a wish to recreate something in particular.

Here is the final sketch:

One of the more challenging parts was the math behind the sketch. First, by using sin and cos together for x and y coordinates, respectively, I was able to trace points on the unit circle. The variable i is used as an angle that varies from 0 to  2π and therefore a full circle is completed. The effect of f is to control the frequency of the oscillation. As f increases, it speeds up the oscillation, making the ellipses move more rapidly from side to side.  I wish I could explain the radius calculation better, but honestly, it was just a random experimentation of plugging in random values and functions until I achieved a smooth transition (a trial and error method more of).

// Looping through 600 iterations to create a series of ellipses
  for (let i = 0; i < TWO_PI; i++) {
    // Calculating the x and y coordinates of the ellipse. Using sin and cos allows for the circular appearance
    let x = (width / 3) * sin(i * f);
    let y = (height / 3) * cos(i * f);
    // Radius is based on a combination of sine and cosine functions involving 't', 'i', and 'f', resulting in a changing size over time.
    let radius = 60 + 100 * sin(12 * sin(t) * sin(i * f));

Another challenge was changing the direction of the animation. I decided to switch directions once f reaches TWO_PI instead of when i does. This was also a personal preference, as I wanted the animation to loop for longer. I then switch the direction and set t and f to 0 to keep the animation from accelerating.

// Check if 'f' has completed a full loop (TWO_PI)
 if (abs(f) >= TWO_PI) {
   // Reverse the direction of motion
   direction *= -1;
   t=0
   f=0
 }

Some ideas for further enhancements could be implementing a smoother transition in the change of directions, as well as enhancing the visual appearance. I do like the fact that the visuals are rather simple and allow for focus on movement, structure, and shape, but I believe this sketch has more potential than only that. Speaking about the aesthetics, I was also quite satisfied with the rotateX(1) line, which enabled me to create a little more depth in the sketch and move slightly beyond the 2D view.

To add, this was actually where I started to notice some interesting dynamics. However, I found this initial pattern a bit too flashy and uncomfortable for the eye. In general, this assignment was an engaging and freehand experimentation with changes in values in the trial and error method until I achieved something that I liked. Here is the first sketch:

For this week’s assignment, I was inspired by the Planar Choreographies, especially this simulation: https://personalpages.manchester.ac.uk/staff/j.montaldi/Choreographies/

The concept of planar symmetry was utterly new to me, however, I found it really fascinating (and a bit addictive even). Here is my own attempt and my sketch:

Apparently, what turned out of the sketch is a system of particles with mutual gravitational attraction. This type of system is chaotic and sensitive to initial conditions, that is why I set all the parameters manually in the code (the positions and velocities of movers and attractors). Even small changes in the starting positions or velocities of the particles lead to significant differences in the long-term behavior of the system. That is how I got to learn that the sensitivity to initial conditions is a characteristic of chaotic systems.

What seemed really interesting to me is that in the beginning the system appears organized, or in more official terms – symmetrical. However, after a while, the system becomes imbalanced and progresses to develop more chaotic qualities. The reason for that is the design of the system. As time progresses, the particles continuously influence each other due to gravity. Small disruptions in their positions or velocities accumulate over time and lead to significant deviations from the initial state.

An additional upgrade that I added was the force of repulsion. Here is how I implemented it in code:

for (let other of movers) {
      // Checking if the current 'mover' (outer loop) is different from the       current 'other' (inner loop)
      if (mover !== other) {
        // Calculating the vector pointing from 'other' to 'mover' and its           distance
        let repulsion = p5.Vector.sub(mover.pos, other.pos); 
        let distance = repulsion.mag();
        // Defining a minimum distance for repulsion and a maximum repulsion           force
        let minDistance = 50; 
        let maxForce = 0.5; 

        // Apply repulsion force if particles are too close
        if (distance < minDistance) {
          repulsion.setMag(map(distance, 0, minDistance, 0, maxForce));
          mover.applyForce(repulsion);
        }
        mover.attract(other);

To calculate the repulsion force, I subtracted the position of ‘other’ from the ‘mover’ to obtain a vector pointing from ‘other’ to ‘mover’, and then  computed the distance between them. I then set a minimum distance that determines when repulsion should occur and a maximum repulsion force to control the strength of the repulsion effect.If the distance between ‘mover’ and ‘other’ falls below the specified minimum distance,  I mapped the repulsion force by scaling the ‘repulsion’ vector based on the distance and the maximum force. This ensures that particles t experience a repulsive force based on the distance at which they encounter each other. Finally, I applied this repulsion force to the ‘mover. This force counteracts the gravitational attraction, preventing particles from getting too close and adding a repulsive behavior to the simulation.

For further improvements, I would be interested to experiment with more movers and attractors placed in various positions. It would be exciting to attempt to create a more stable choreography, make it appear 3D or perhaps to add some additional visual effects, like color changes or to play around with connecting lines.

 

This week’s project was inspired by ducks and their swimming movement. Here is a short calming 5 hour video of the phenomenon in question:

Here is the sketch:

As I was scrolling through my camera roll, I noticed that I had quite a few videos of ducks swimming by the shore of a pond. I remembered the mouse tracking example task that we did last class, and it occurred to me that the walker was moving in a similar fashion like the ducks following a human on the shore who is holding a piece of bread. I thus wanted to alter the code of the task to simulate a group of swimming ducks.

To translate this idea into code, I decided to create a scenario where the ducks were drawn towards a fish instead of a human with bread, adding a more natural and engaging touch. Additionally, I aimed to introduce a bit of unpredictability to mimic real-life scenarios by randomizing the number of ducks with each sketch as they swim in both smaller and larger groups. Since they often come together in one spot, I wanted them to form circular patterns while changing positions.

In order to achieve this, I used object-oriented programming to create the duck objects, and vectors to simulate their movement. For instance, I employed vectors to determine the distance between each duck and the fish cursor. This enabled me to simulate the ducks’ natural tendency to swim toward a target, just like real ducks follow food. By calculating these distances and adjusting the ducks’ directions accordingly, this behavior was replicated in code.

The part of the code for which I was proud of was the snipet where I tried to make the ducks avoid collisions. To achieve that I needed to calculate a ‘pushForce’ vector that points away from the current duck, which was then assigned as a new acceleration vector. Here is the snipet:

avoidCollisions(ducks) {
    let avoidance = createVector(0, 0);
    
    //Looping through each of the ducks
    for (let i = 0; i < ducks.length; i++) {
      // Checking if the current duck being checked is not the same as this duck
      if (ducks[i] !== this) {
        // Calculating the distance between this duck and the current duck in the loop
        let distance = p5.Vector.dist(this.position, ducks[i].position);
        // Checking if the distance is less than the desired distance
        if (distance < minDistance ) {
          // // Calculating a 'pushForce' vector that points away from the current duck
          let pushForce = p5.Vector.sub(this.position, ducks[i].position);
          // Setting the magnitute
          pushForce.setMag(0.1); 
          // Adding the 'pushForce' vector to the 'avoidance' vector
          avoidance.add(pushForce);
        }
      }
    }
    // Changing the acceleration to the 'avoidance' vector
    this.acceleration = avoidance;
  }

Although the movement of the fish was not my main concern, I was very satisfied with how it turned out. The little glitches that occur during the cursor movement actually appear similar to how smaller fish actually tend to have uneven swimming patterns and often do sudden turns and unexpected movements.

For further improvements, I would love to make the ducks also swim in a V like shape, where one of them would take the lead and others would stay a little behind forming the V. Another idea could be to simulate the ducks going underwater and disappearing for a while why they attempt to catch the fish. Of course, it would also be a big plus to improve the visual appearance of the ducks, and perhaps simulate some water movement as well.

For the first week’s project, I decided to implement a self-avoidant walk and boost it with changes in HSB according to the walker’s position on the 2D plane.

THE SKETCH:

https://editor.p5js.org/llluka/sketches/iYn-Ng2tv

The canvas is split into a grid of cells, with each square indicating a possible location for the self-avoiding random walker. As a result, a 2D array was formed to track the walker’s movement, with every element corresponding to a cell on the canvas. Such structure ensures that the walker does not revisit previously occupied cells and moves in an intricate pattern on the canvas. The walker begins its movement from the center of the canvas, and its movement is decided randomly. The path is finite, depending on how fast the walker ends up in a position where all of the neighbor cells are already occupied.

The coloring of the walker’s path is dynamically generated based on the walker’s position, both x and y coordinates, creating different gradients of hue, saturation, and brightness on different parts of the canvas. Hue is influenced by both x and y, while saturation varies vertically, and brightness varies horizontally. Here is the code I used to achieve that:

  // Influencing the hue based on both x and y positions
  let hue = map(x + y, 0, cols + rows, 0, 360);

  // Adjusting the saturation based on y so that the saturation varies vertically on the canvas.
  let saturation = map(y, 0, rows, 100, 255);
  
  // Adjusting brigthness based on x so that the brightness varies horizonatally on the canvas
  let brightness = map(x, 0, cols, 100, 255);

  // Set the stroke color using HSB color mode with adjusted saturation and brightness
  stroke(hue, saturation, brightness, 200);

For future advancements for this project, I would imagine implementing a backtracking algorithm that would allow the walker to backtrack and retrace its steps when it encounters a dead end. In such a way the walker’s journey could be extended, resulting in longer patterns. Nevertheless, this project was a great opportunity to practice 2D arrays. I remember making board games in my Intro to Computer Science class, and it was exciting to implement the same structures but in another language.

Here are a few images of the more beautiful patterns that occurred:

In the introductory chapter computer scientist and author Gary William Flake draws attention to how computational science can be used to understand the complexities of the natural world. He begins by highlighting how science, mathematics, and computer algorithms are interconnected and how powerful the combination of these fields can be in comprehending natural phenomena. I found it interesting how computational techniques and their capacity to allow for visualization, pattern recognition, and prediction provide a powerful lens through which we can uncover the underlying beauty and complexity of the universe. The author’s point that computational science has increased interdisciplinary collaboration unveiled a fresh layer of insight. Although that was an apparently simple and agreeable argument, it made me reflect on how computation promotes a holistic understanding of the universe’s beauty and complexity by drawing on insights from different scientific domains.

Flake’s emphasis on the crucial significance of computational science for interdisciplinary collaboration made me think how pressing scientific challenges such as climate change are being addressed today. The intricacies of an issue like climate change require expertise from diverse disciplines, including biology, chemistry, ecology, and atmospheric science in order to establish computer models for exploration and prediction purposes. As all of the mentioned disciplines are usually quite specialized and thus often isolated from each other, computer modeling in this case is one of the primary factors that unites them and makes the accounting for the intricate interplay of various environmental factors possible. Therefore, climate change supports this Flake’s argument on how computational science promotes a more holistic and multidisciplinary understanding of natural phenomena.

Thinking further, another widespread issue besides the single-lens approach that science often encounters is the lack of funding and resources. Here computer science serves a critical role as well, as the promotion of collaborative projects has the potential to attract support from a broader spectrum of funding sources and organizations as multiple fields converge. The enormous potential of computational science to address complex global issues can be fully unlocked by this financial and resource synergy, which can significantly accelerate research and innovation. This in turn makes interdisciplinary collaboration an essential tactic for overcoming current greatest challenges.