Category: F2023 – Aya

Code: https://editor.p5js.org/bdr/sketches/Vnv5bkHdK

Concept:

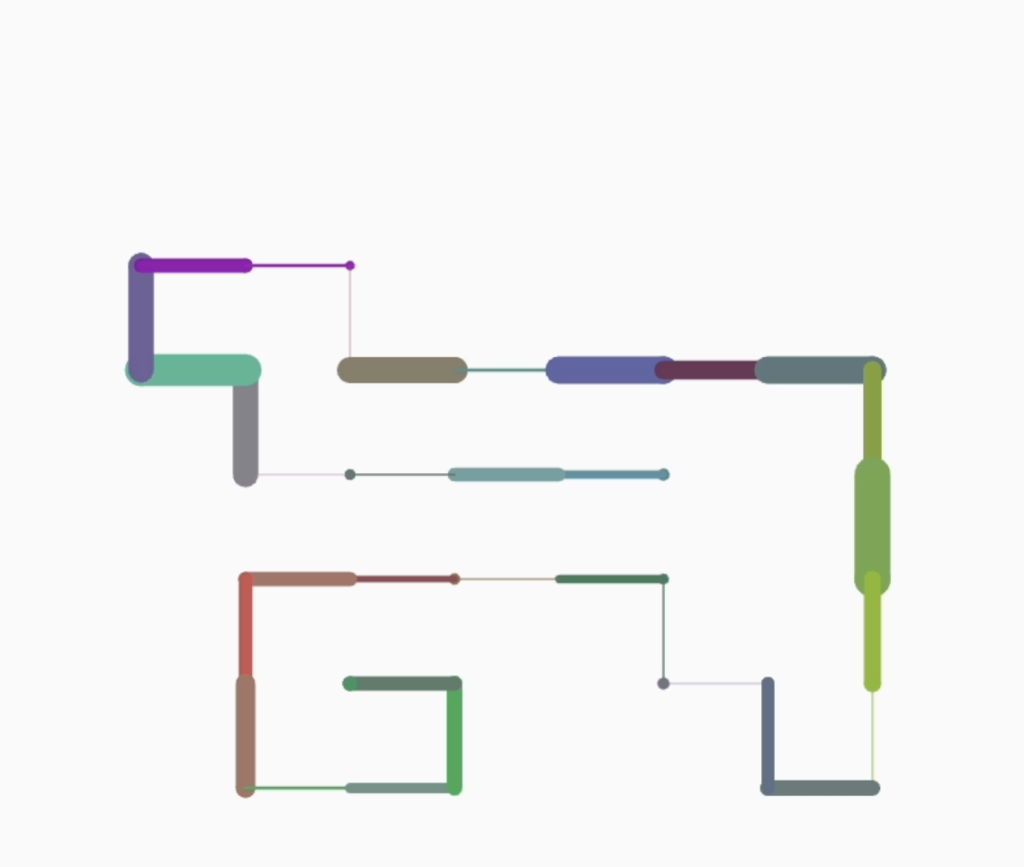
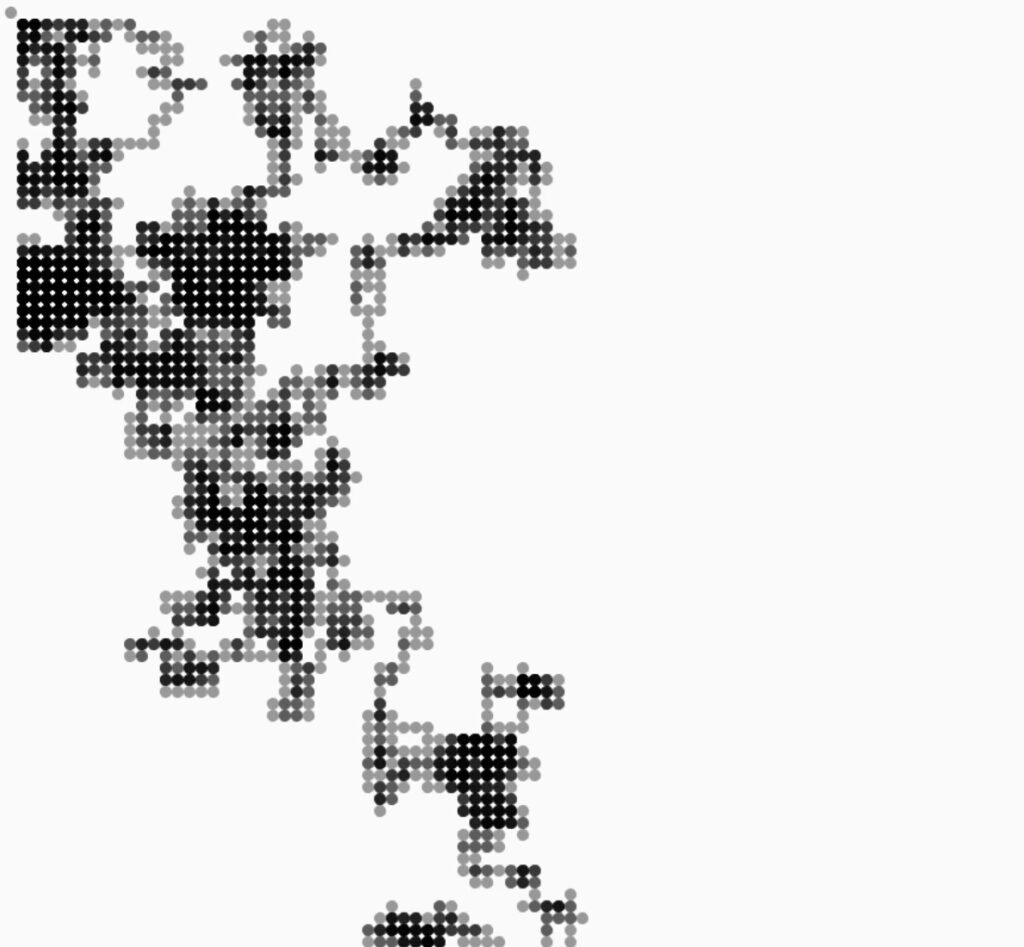
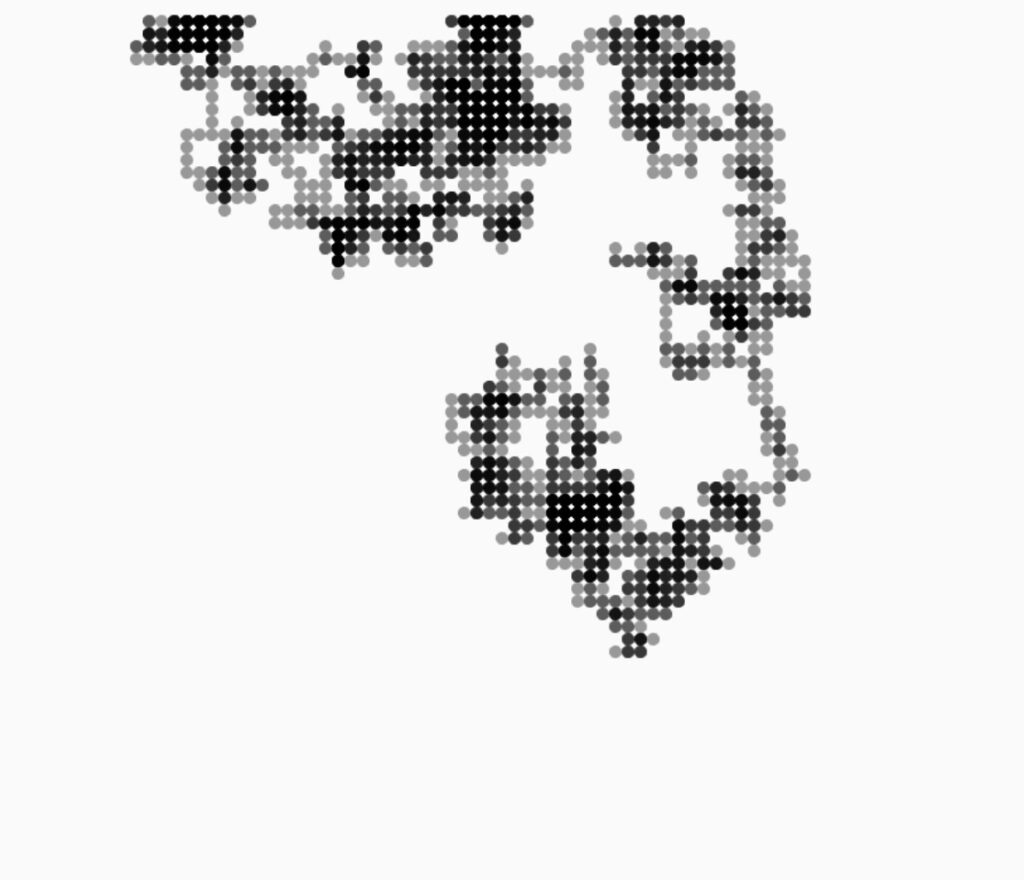
Connections combines two concepts: Levy flight motion and dynamic bezier curve connections between particles. Levy flight is a type of random walk where the step length follows a heavy-tailed probability distribution, resulting in a long erratic movement. It represents a dynamic system of particles moving within the canvas, with real-time changing edges connecting them. My sketch draws inspiration from concepts in computational art to explore the interplay between randomness and controlled forms in a dynamic particle system.

Steps:

View post on imgur.com

View post on imgur.com

Code Walkthrough:

A ‘Particle’ class encapsulates the behavior and properties of individual particles. Each particle is initialized with a random position (x,y) within the canvas and a random color with alpha transparency. The particles move according to Levy flight motion and can change direction when they come into close proximity to each other.

Particle Movement – Levy Flight:

Using the update() function, a random length and direction is calculated and is reflected on the particle’s movement. Since stepDirection is a random angle, cos(stepDirection) and  sin(stepDirection) generate random values between -1 and 1. These values are then multiplied by stepLength, which is a random value as well. The use of cosine and sinus ensures that the particle can move in any direction as stepDirection can take any value between 0 and 2π.

// Levy flight movement
update() {
  let stepLength = random(3);
  let stepDirection = random(TWO_PI);
  this.x += cos(stepDirection) * stepLength;
  this.y += sin(stepDirection) * stepLength;

  // Keep particles within bounds
  this.x = (this.x + width) % width;
  this.y = (this.y + height) % height;
}

Particle Appearance:

The display() method draws each particle as a white ellipse with random alpha to create a glowing effect.

Particle Interaction:

As the particles come too close to each other, they both change their respective directions. It is handled by the changeDirection() function.

Particle Connection – Lerp:

If two particles come within a certain distance, a bezier curve is drawn between them. Linear interpolation is used twice for each pair of connected particles: once to determine the position of the first control point (x1,y1) and again for the second control point (x2,y2). It allows for fine-tuning the curvature of the bezier curve between them.

// Control points for bezier
let control1X = lerp(particles[i].x, particles[j].x, 0.1);
let control1Y = lerp(particles[i].y, particles[j].y, 0.4);
let control2X = lerp(particles[i].x, particles[j].x, 0.9);
let control2Y = lerp(particles[i].y, particles[j].y, 0.9);

// Combines the colors of the particles it connects
stroke(lerpColor(particles[i].color, particles[j].color, 0.5));
bezier(particles[i].x, particles[i].y, control1X, control1Y, control2X, control2Y, particles[j].x, particles[j].y);

The color of each bezier curve is a combination of the colors of the two connected particles, creating a smooth color transition along the curve (using Lerp again).

Challenges:

Achieving a balance between randomness and control in the particle movement can be tricky as an excess in randomness can result in chaos and unpredictable behavior. I was able to do that by fine-tuning these parameters and following a trial and error process.

Possible improvements:

• Particle attraction: add forces of attraction
• User Interaction: let the user interact through clicks or mouse movement

CONCEPT

So, for this week’s coding assignment, I tried to implement the self-avoiding walk. I am a mathematics major too and I wanted to explore a mathematical concept through what we’ve been learning in class. In mathematics, a self-avoiding walk (SAW) is a sequence of moves on a lattice path that does not visit the same point more than once. To make it more interesting and look like a computer chip, or gaming area (of pac-man, say), or a network of pipelines, or points and paths on a map, I played around with the color() and strokeWeight() property of the lines and dots I was plotting. With someone randomness using noise as we learnt in class, I was able to achieve interesting and fascinating results!

EMBEDDED SKETCH

WORKING VIDEO

See my self-avoiding walk walking! 🙂

KEY TECHNICAL ASPECTS

There are 2 code snippets I would like to highlight:

1. First is the core concept of the self-avoiding walk – how it chooses which direction to go next and how it avoids itself. For this, I populated an array with available spaces for the walker to move on the basis of which vertices were already visited or not. And then, instead of randomly choosing from numbers between 1-4, the walker randomly chooses a place to go from this array of available spaces.

this.matrix = []; // holds position where all the walker has been --> initially populated to false, changed to true when walker visited that spot

// for populating the spaces available to walker
let options = []; // to store which options available to go to
    if (this.isValid(this.x+1, this.y)) //i.e. right available space
      options.push(0);
    if (this.isValid(this.x-1, this.y)) //i.e. left available space
      options.push(1);
    if (this.isValid(this.x, this.y+1)) //i.e. up available space
      options.push(2);
    if (this.isValid(this.x, this.y-1)) //i.e. available space
      options.push(3);

// for choosing where to go from the available spaces
let choice;
    if (options.length > 0) {
      choice = (random(options));
      if (choice == 0)
        this.x++; // go right
      else if (choice == 1) 
        this.x--; // go left
      else if (choice == 2)
        this.y++; // go up
      else if (choice == 3)
        this.y--; // go down
      this.matrix[this.x][this.y] = true; // mark this place as visited
    }
    else {
      print("OVER");
      // text("OVER", width/2 - 10, height/2);
      noLoop();
    }

isValid(i, j) { // checks if this matrix space / vertex is available to visit or not
    if (i < 0 || j < 0 || i >= num_rows || j >= num_cols)
      return false;
    return (!this.matrix[i][j]);

2. The second thing I want to highlight is my code for random colours and dot sizes.

// for randomizing dot size based on random gaussian
let w = randomGaussian(5,3);
    strokeWeight(w);
    
// for randomizing stroke color based on noise
    let n1 = noise(t);
    let n2 = noise(t+50);
    let n3 = noise(t+100);
    t += 0.5;
    let c1 = map(n1, 0, 1, 0, 255);
    let c2 = map(n2, 0, 1, 0, 255);
    let c3 = map(n3, 0, 1, 0, 255);
    let c = color(c1,255-c2,c3)
    
//plot the point / dot
    stroke(c);
    point(this.x * this.step + this.step/2, this.y * this.step + this.step/2);

// plot the line
    strokeWeight(1);
    line(this.prev_x * this.step + this.step/2, this.prev_y * this.step + this.step/2, this.x * this.step + this.step/2, this.y * this.step + this.step/2);

IMAGE GALLERY

Some more drawings that occurred in the process:

 

FURTHER DEVELOPMENTS

Currently, the self-avoiding walk gets stuck once it reaches a point and has no more places to go. It has travelled to all its neighbouring points and since it is self-avoiding, it can’t cross itself again. This is what we call a ‘dumb’ self-avoiding walk, which just randomly chooses a point to move to next without thinking about the future – whether this will lead me to continue on a longer path or this move will get me stuck. Hence, the next step would be to implement a ‘smart’ self-avoiding walk, which can keep track of whenever it gets stuck and go back and choose a better move which will allow it to continue for longer. The algorithm for this is rather complicated as it requires backtracking and dynamic programming, but still doable and somewhat similar to the computer algorithms for solving mazes.

COMPLETE CODE

https://editor.p5js.org/shreyagoel81601/sketches/0ooUuQdcW

1- Code Production:

Inspiration Behind the Project: Aside from this project being an assignment, I was inspired to implement this virtual orchestra using the skills learned in class from this an old new article from 2008 on the world’s first virtual online collaborative orchestra that allowed musicians all over youtube to collaborate and create a musical masterpiece. I found it particularly interesting, because when I think of such technological advancements, interactivity and collaborations I associate them to more recent projects, however this project was initiated back in 2008!

https://googleblog.blogspot.com/2008/12/calling-all-musicians-join-youtubes.html

Brief Description: In this program, I created a walker that has a 50% chance of the it’s patterns being drawn based on the location in which the user hovers the mouse, and the other 50% chance is simply based on the basic uniform randomness of the walker. (Shown in code below)

Alongside this movement, I also implemented an orchestra like user interaction by including an audio file that plays based on where the user hovers over the screen. Instead of using just shapes, I used an orchestra man instead of the circle, and an orchestra background for better visualization.

    let r = random();
    if (r < 0.5) { //Here we have created a 50% chance of the walker's patterns being drawn based on the location in which the user hovers the mouse 
      this.x=mouseX;
      this.y= mouseY

    } else {
     let choice = floor(random(4)); // and for the other 50% chance  the walker continues to move randomly by taking a random number from 1 to 4 and ensuring its an integer value
    if (choice === 0) {
      this.x+=20; //note that I used plus 20 so the random movement can be more obvious 
    } else if (choice == 1) {
      this.x+=20;
    } else if (choice == 2) {
      this.y+=20;
    } else {
      this.y+=20;
    }

    }

https://editor.p5js.org/ea2749/full/_LsBNgndx

2- Response Paper:

In the first chapter of the book Computational Beauty of Nature, author Gary William Flake begins by delving into the concept of looking at the universe through reductionism and how it is a concept that is definitely applied to various fields of sciences. However soon after setting the definition of reductionism and providing examples, Flake goes on to argue that at some point reductionism must stop for science to advance. This reminded me of a biology topic we had discussed in one of our classes. Scientist’s Gregor Mendel and Thomas Hunt Morgan research had more of a reductionist and gene-centric view studies on inheritance of traits in fruit-flies, which led to many discoveries however at some point became problematic because over complex view of inheritance allowed for scientists to ignore the interactions between genes, proteins, and environmental factors.

An example Flake mentioned that really stood out to me was the Psychologists use certain computer simulations to better analyze cognitive models of the brain. Flake includes other examples as cited: “Physicists study the flow of plasma and the annealing of metals. Economists have modeled various types of economies,”. What would have been better perhaps is of Flake further delved into at least one of applications of computer stimulations, rather than just listing them, this slightly weakens his argument, especially since he mentions that his book’s focus is primarily on computational topics. In fact due to the vagueness of his examples, I began to wonder whether the use of computer simulations can lead to flaws in cognitive models or any scientific model in general?

 

Computational Beauty of Nature presents a nuanced perspective on the concept of reductionism and its relevance in scientific research, sparking reflection on the nature of our understanding of complex systems. It underscores the balance between recognizing the benefits of reductionism and acknowledging its limitations. In Biology, reductionism has proven successful in studying life forms at various organizational levels, from whole organisms down to tiny molecules. Yet, while valuable, reductionism may not always give us the full picture. Understanding how things interact and the emergent properties that arise is as crucial in scientific exploration as tracing them back to the quantum level.

It is worth noting the author’s subtle inclination towards favoring a more holistic perspective on understanding complex systems as he continuously hints at possible limitations in the reductionist approach. Despite the bias, the reading encourages a deeper appreciation for the different natures of scientific investigation and suggests that embracing various perspectives can enrich our comprehension of the world’s intricacies. As for personal beliefs, the reading didn’t necessarily change them but prompted some introspection. I believe that combining both methodologies will result in a much richer understanding of the world around us. However, it did leave me with thought-provoking questions regarding how incompatible or complementary reductionism and holism are together, and if a balance is realistic.

The first chapter of “The Computational Beauty of Nature” serves as the cornerstone for delving into the realm of computational aesthetics. It lays down the fundamental concepts, highlighting the crucial role of mathematics in our comprehension of natural beauty. Additionally, it underscores the multidisciplinary character inherent in this field, where mathematics, computer science, and other disciplines converge.

In this chapter, the notion of algorithmic information theory is introduced as a powerful framework for grasping the patterns found in the natural world. It posits that these patterns can be succinctly encapsulated by algorithms, offering a means to measure their complexity. This concept, in turn, has profound implications for our perception and quantification of beauty within our surroundings.

However, it’s important to note that this approach has its own set of challenges. The computation of algorithmic complexity for extensive datasets or intricate systems can often become intractable, hampering its applicability in real-world scenarios that demand efficient and scalable methods. Furthermore, AIT has faced criticism for its limited empirical validation in practical situations.

Despite its theoretical elegance, AIT’s capacity to provide precise predictions and elucidate intricate natural phenomena remains a subject of ongoing exploration. Its interdisciplinary nature, while advantageous in its breadth, can also present difficulties in achieving deep specialization in specific domains.

Concept: 

My concept this week is “RADAR”. It is an art piece in which there are multiple walkers located randomly on the canvas and walk towards the cursor and then after a few seconds they scatter back to their initial positions. There are horizontal and vertical lines which gives the image the feel of a radar.

Sketch: 

https://editor.p5js.org/mi1171/full/wgCqaP_wT

step(){
    let stepvar = (random(1));

    if(stepvar < 0.6){
      if(bool == true){
      if(mouseX>=this.x){
      this.x++} if(mouseX<this.x){
        this.x--
      }
        if(mouseY>=this.y){
      this.y++}
        if(mouseY<this.y){
        this.y--
      }
    }else{
      if(this.initialx>=this.x){
      this.x++}
      if(this.initialx<this.x){
        this.x--
      }
        if(this.initialy>=this.y){
      this.y++}
        if(this.initialy<this.y){
        this.y--
      }
    }
    } else if(stepvar < 0.7){
      this.y++
    } else if(stepvar < 0.8){
      this.x--
    } else {
      this.y--
    }
    this.x = constrain(this.x,0,width-1);
    this.y = constrain(this.y,0,height-1);
    
    if(this.r<= r2){
      this.r++
    }else{
      this.r--
    }
    
     if(this.g<= g2){
      this.g++
    }else{
      this.g--
    }
    
     if(this.b<= b2){
      this.b++
    }else{
      this.b--
    }
}

This is my step function, the part I’m particularly proud of is how I manage to make the walkers go back to their initial positions after the bool variable becomes true. (This variable flips every 400 frames)

Challenges:

In this week’s assignment, I had 1 main issue, which was the lag caused by the code. I decided to decrease the number of walkers I had from 200 to 100, which greatly decreased the amount of lag in the sketch while still maintaining the integrity of the art piece.

Future Improvements: 

There are some improvements that can be made to this assignment. For example, I can add a line that rotates and ‘detects’ the circles. When detected the circles can increase in opacity, then slowly decrease until the line touches them again. 

Reductionism is a method of breaking down complex concepts into simpler, more understandable bits. It is a highly effective technique of learning how certain individual components work, but it does not always convey the complete picture. A concept must also be viewed in relation to its interaction with other concepts or with its external environment. Those relationships that an organism has with its environment can only be explored at a higher level of examination. Each element of a system can interact with one another, resulting in emergent unique traits that cannot be explained just by reductionism. Holism is a way of perceiving the world that does not focus on the individual but on the system that is made up of individuals. Using this strategy can lead to an increased understanding of how the world works since, in many circumstances, the system becomes bigger than the sum of its parts. Only via a comprehensive understanding can we find and connect these seemingly diverse domains. To achieve a more thorough understanding of the world, I feel that both reductionism and holism are necessary. These 2 methods synergize with one another, when we learn about how an individual component of a system works, then we can also gain a deeper understanding of how the whole system operates and vise versa.

Using a holistic perspective, we discovered that ideas from one field, like animal flocking, had similarities in another, like financial markets. When we view the world from a more holistic perspective, we find surprising overlaps and patterns that cut across traditional academic disciplines. Principles from one field might inspire solutions in another, so it’s helpful to think across disciplines to generate new ideas. Also, holism exposes the universality of some patterns, such as self-organization and adaptation, across other systems. With this understanding, we may foster the growth of new interdisciplinary areas and promote innovation. When confronting problems with many interconnected components, such as climate change or healthcare, which necessitate an multidimensional approach for both technical and societal dimensions, a holistic perspective is crucial.

Introduction

The Walker is an interactive p5.js project that creates a constantly morphing creature that moves in random directions on a canvas. This project utilizes JavaScript and the p5.js library to generate a visually intriguing and ever-changing artwork. In this documentation, we will provide a detailed description of what the Walker does, what the user can expect, and any interactive elements involved.

Project Description

What It Does

The Walker is an abstract creature that appears to be walking across the canvas. It constantly changes its shape, giving it an amorphous and unpredictable appearance. The key features of the Walker project are as follows:

1. Random Movement: The Walker moves in random directions, making it appear as if it is wandering aimlessly across the canvas.
2. Mouse Interaction: There is a 50% chance that the Walker will move towards the mouse cursor’s position. When this happens, it appears as though the creature is attracted to the mouse.
3. Shape Morphing: The creature’s shape is continually changing. It starts with a predefined shape made up of random vertices, and these vertices are updated randomly, causing the creature to morph over time.

User Interaction

The user’s interaction with the Walker project is minimal but plays a crucial role in shaping the creature’s movement. Here’s what the user can do:

• Mouse Movement: When the user moves their mouse cursor within the canvas, the Walker may respond by moving towards the mouse cursor with a 50% probability. This interaction creates a dynamic relationship between the user’s cursor and the creature’s movement.

Implementation

Walker Class

The Walker is implemented as a JavaScript class with the following methods:

• Constructor: The constructor sets up the initial position of the Walker at the center of the canvas and initializes the creature’s shape with a random set of vertices.
• step(): This method controls the Walker’s movement. It calculates a random number to determine whether the Walker should move towards the mouse cursor or in a random direction. If the decision is to move towards the mouse, it adjusts the position of the Walker accordingly. Otherwise, it moves the Walker randomly. The Walker’s position is constrained within the canvas boundaries.
• display(): The display() method is responsible for rendering the Walker on the canvas. It draws the creature as a shape with constantly morphing vertices.
• updateBounds(): This method randomly updates the positions of the creature’s vertices, causing it to morph and change shape.

Setup and Draw Functions

In the p5.js setup function:

• The canvas is created with a size of 400×400 pixels.
• The background is set to a light gray color (RGB 220, 220, 220).
• An instance of the Walker class is created.

In the p5.js draw function:

• The step() method of the Walker is called, updating its position.
• The display() method of the Walker is called to draw the creature on the canvas.

Demo

Full-source code

Conclusion

The Walker project is an interactive P5.js artwork that combines randomness and user interaction to create an ever-changing and visually intriguing creature. Users can observe the creature’s unpredictable movement and, through their mouse cursor, influence its direction. This project serves as an example of how programming and creativity can come together to produce interactive and captivating visual experiences.

The ideas presented in this chapter really resonate with me because they emphasize the beauty of simplicity, in explaining phenomena. The examples, like how ant colonies function or how basic rules can account for patterns in nature show us that the world operates on principles. This reinforces my belief in the elegance of simplicity and its role in helping us understand the complexities of life.

Moreover the chapter highlights the significance of collaboration. It makes me think about how scientific research’s evolving. As someone who values approaches it’s reassuring to witness how computers have bridged the gap between theory and experimentation fostering collaboration among scientists from fields. This convergence has potential to unlock insights and solutions to complex problems by harnessing expertise from various disciplines.

However it also raises questions about finding a balance between specialization and interdisciplinary cooperation. While specialization allows for exploration, within a field this chapter suggests that breakthroughs often result from collaboration and sharing ideas across disciplines. It leaves me contemplating how we can strike the balance as we pursue understanding and problem solving – ensuring that we leverage both specialized expertise and interdisciplinary synergy.

In the introductory chapter computer scientist and author Gary William Flake draws attention to how computational science can be used to understand the complexities of the natural world. He begins by highlighting how science, mathematics, and computer algorithms are interconnected and how powerful the combination of these fields can be in comprehending natural phenomena. I found it interesting how computational techniques and their capacity to allow for visualization, pattern recognition, and prediction provide a powerful lens through which we can uncover the underlying beauty and complexity of the universe. The author’s point that computational science has increased interdisciplinary collaboration unveiled a fresh layer of insight. Although that was an apparently simple and agreeable argument, it made me reflect on how computation promotes a holistic understanding of the universe’s beauty and complexity by drawing on insights from different scientific domains.

Flake’s emphasis on the crucial significance of computational science for interdisciplinary collaboration made me think how pressing scientific challenges such as climate change are being addressed today. The intricacies of an issue like climate change require expertise from diverse disciplines, including biology, chemistry, ecology, and atmospheric science in order to establish computer models for exploration and prediction purposes. As all of the mentioned disciplines are usually quite specialized and thus often isolated from each other, computer modeling in this case is one of the primary factors that unites them and makes the accounting for the intricate interplay of various environmental factors possible. Therefore, climate change supports this Flake’s argument on how computational science promotes a more holistic and multidisciplinary understanding of natural phenomena.

Thinking further, another widespread issue besides the single-lens approach that science often encounters is the lack of funding and resources. Here computer science serves a critical role as well, as the promotion of collaborative projects has the potential to attract support from a broader spectrum of funding sources and organizations as multiple fields converge. The enormous potential of computational science to address complex global issues can be fully unlocked by this financial and resource synergy, which can significantly accelerate research and innovation. This in turn makes interdisciplinary collaboration an essential tactic for overcoming current greatest challenges.