Assignment 3 – Kaleidoscope

This sketch is a kaleidoscopic illustration of movers and attractors. My main inspiration is a combination of the picture above and a mix of effects I used in one of my motion graphics/VFX projects. I wanted to recreate a sample that captures both feelings at once.

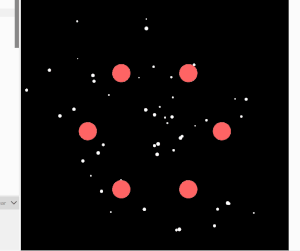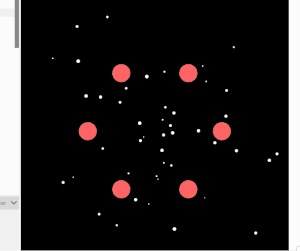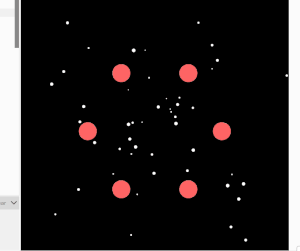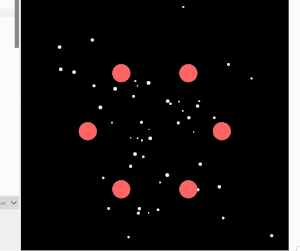
I started this sketch by placing circular attractors as shown in the image.

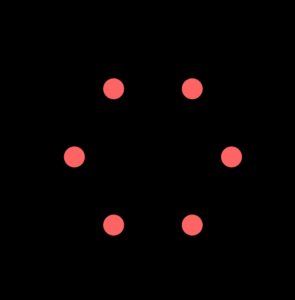
I wrote code that creates a circular arrangement of attractor points around a center position.

  for (let i = 0; i < numAttractors; i++) {
    let angle = (TWO_PI / numAttractors) * i;
    let x = centerX + cos(angle) * attractorRadius;
    let y = centerY + sin(angle) * attractorRadius;
    attractors.push(new Attractor(x, y, 20));
  }
}

This loop divides the circle into segments, each iteration multiplies by i to get the angle for that specific attractor. For x and y positions, I use polar-to-cartesian coordinate conversion as shown in the code.

Then I added movers and I applied the forces to the movers such that their position is affected by the attractors.

For this effect I take inspiration from this code.

So basically, the kaleidoscope effect happens because every single object gets drawn (numAttractors) times instead of just once. The trick is that before drawing each copy, the code rotates the entire coordinate system around the center of the canvas by increments of 60 degrees (since 360 deg ÷ 6 = 60 deg). It does this by moving the origin to the canvas center, rotating, then moving it back, and finally drawing the object at its actual position. But because the whole coordinate system has been rotated, what you actually see is the object appearing in six different spots arranged symmetrically around the center, like looking through a kaleidoscope. The cool part is that the physics simulation itself, only happens once for each object, but visually you see six reflections of everything. So when a mover orbits an attractor, all six of its mirror images orbit simultaneously.

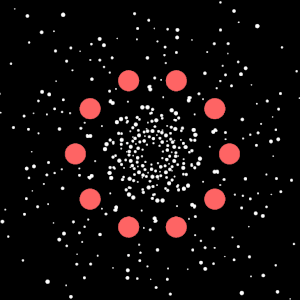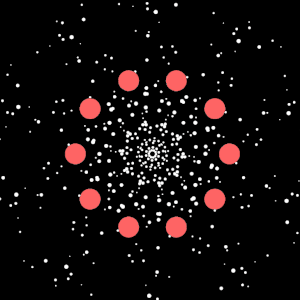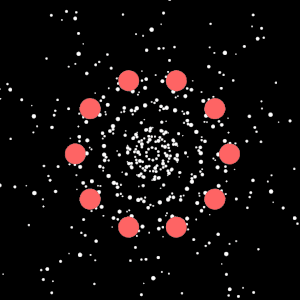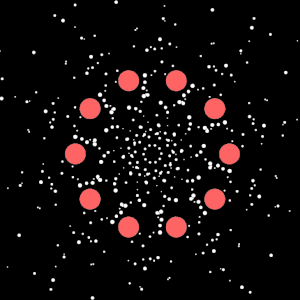
For example, the number of movers in this sketch is 1, but it gets reflected 5 times

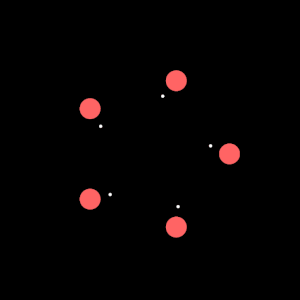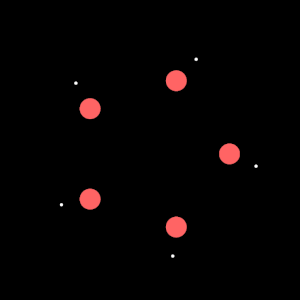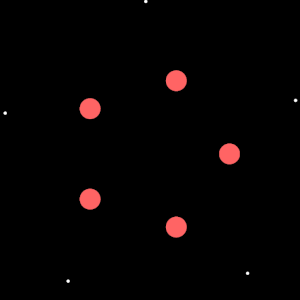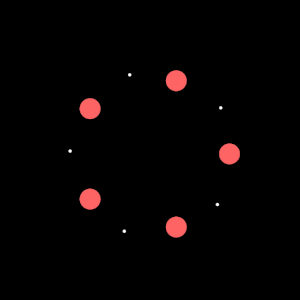
Here’s the code responsible for the kaliedoscope effect

for (let i = 0; i < symmetryFold; i++) {
  push();
  translate(width / 2, height / 2);      // move origin to center
  rotate((TWO_PI / symmetryFold) * i);   // rotate by incremental angle
  translate(-width / 2, -height / 2);    // move origin back
  circle(this.position.x, this.position.y, size);  // draw at original position
  pop();
}

I then made some really interesting changes here that make the pattern way more complex and controlled. I added this clever touch of four “corner attractors” placed at each corner of the canvas with higher mass , which act like gravitational anchors that influence the overall flow and create an effect of repulsion. I also added a visibility toggle (showAttractorsRepeller) so I can hide the attractors if I just want to see the trails. Speaking of trails, I changed the background to fade super slowly with background(0, 1) instead of clearing completely each frame, which creates these motion trails that build up over time. And finally, I made the movers wrap around the screen edges, if one goes off the right side it reappears on the left, which keeps the pattern continuous and prevents movers from escaping the canvas entirely.

Then I hit the jackpot. By changing one of the corner attractors mass, I create really interesting kaleidoscopic effects as shown in the gif below

Then by playing with the number of attractors I achieve really compelling visual effects like this

Sketch

To get the most out of this sketch, please manipulate the parameters I indicated at the top of the code. There’s something so super satisfying with watching those patterns slowly get created.

The part I’m most proud of is how I implemented the radial symmetry to create that kaleidoscope effect. I only spawn a couple of movers in one “wedge” of the canvas, like a single slice of pizza, and then mirror them automatically across however many symmetry folds I’ve set instead of simulating physics for dozens of particles. The magic happens in the show() methods where I loop through each symmetry fold, rotate the coordinate system incrementally around the canvas center, and draw the same object multiple times at different rotational positions. So when I have 10 attractors arranged in a circle, I also get 10-way symmetry, meaning my 2 actual movers appear as 20 visual copies. It’s incredibly efficient because the physics calculations only happen once per real mover, but the visual output looks way more complex and mesmerizing. The whole system is tied together by making symmetryFold equal to numAttractors.

  show() {
    fill(255, 100, 100);
    noStroke();
    
    // draw attractor with radial symmetry
    for (let i = 0; i < symmetryFold; i++) {
      push();
      translate(width / 2, height / 2);
      rotate((TWO_PI / symmetryFold) * i);
      translate(-width / 2, -height / 2);
      circle(this.position.x, this.position.y, this.mass * 2);
      pop();
    }
  }
}

Moving forward, I’d love to add some interactivity so I can manipulate the system in realtime, maybe clicking to add new attractors or repellers, or using the mouse to adjust the gravitational constant and see how it affects the flow. I’m also thinking about implementing color gradients based on velocity or distance from the center, which would add another layer of visual depth to the trails. I did try this actually but it looked so bad I had to remove it. I also tried making the hue based on the velocity but that also looked bad. It would be cool to experiment with different symmetry modes too, like switching between radial symmetry and bilateral symmetry on the fly, or even adding a mode where the symmetry fold changes dynamically over time to create evolving patterns. Finally, adding some kind of preset system where I can save and load different attractor configurations would make it way easier to explore different aesthetic possibilities without manually tweaking parameters every time.

Sketch

Leave a Reply Cancel reply