Category: S2026 – Jack

Concept and Inspiration

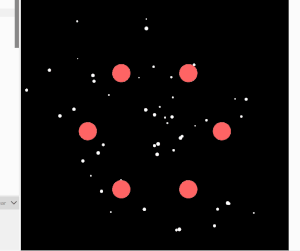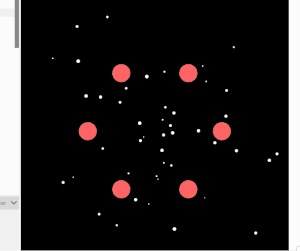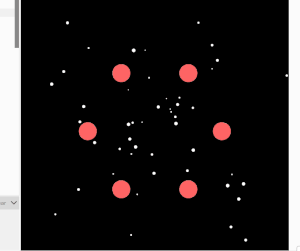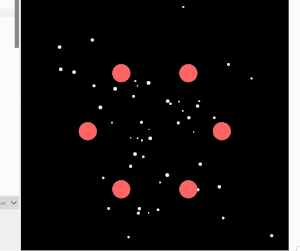
This project simulates particles moving through a maze using forces rather than bouncing off walls. Each particle is pulled toward a target point but pushed away by invisible walls shaped like rectangles. A gentle random force based on Perlin noise makes their movement look natural and smooth. I was inspired by sci-fi movies like Tron and by art that uses flowing patterns. The goal was to create flowing, energy-like paths that happen naturally from how the forces work together, not from fixed paths.

Code Organization and Naming

The code is organized into clear components: a Particle class manages position, velocity, acceleration, and trail rendering; a Wall class defines rectangular obstacles; and dedicated functions handle forces (applyGoalAttraction(), applyWallRepulsion(), and applyTurbulence()). This separation keeps the program modular and readable. Variable and function names are descriptive — like goalStrength, wallRepelStrength, and applyWallRepulsion — to make the code’s purpose immediately clear without confusion.

Code Highlights and Comments

I’m particularly proud of the wall repulsion system, which calculates the closest point on each wall rectangle to the particle and applies a smoothly scaled repulsion force. This method avoids abrupt collisions, allowing particles to gently slide away from walls rather than bouncing harshly. As a result, the particle trails form elegant, curved paths that reveal the flow of forces shaping their motion. The code is carefully commented, especially in the tricky parts like the closest-point calculation and force scaling, to clearly explain the math and logic behind this smooth, natural movement.

// push particles away from rectangles
function applyWallRepulsion(p) {
  for (let w of walls) {

    // find closest point on wall rectangle
    let closestX = constrain(p.pos.x, w.x, w.x + w.w);
    let closestY = constrain(p.pos.y, w.y, w.y + w.h);

    let closestPoint = createVector(closestX, closestY);

    // vector from wall to particle
    let diff = p5.Vector.sub(p.pos, closestPoint);
    let d = diff.mag();

    // only repel if within influence distance
    if (d < 40 && d > 0) {
      diff.normalize();

      // closer = stronger push
      let strength = wallRepelStrength / d;
      diff.mult(strength);

      p.applyForce(diff);
    }
  }
}

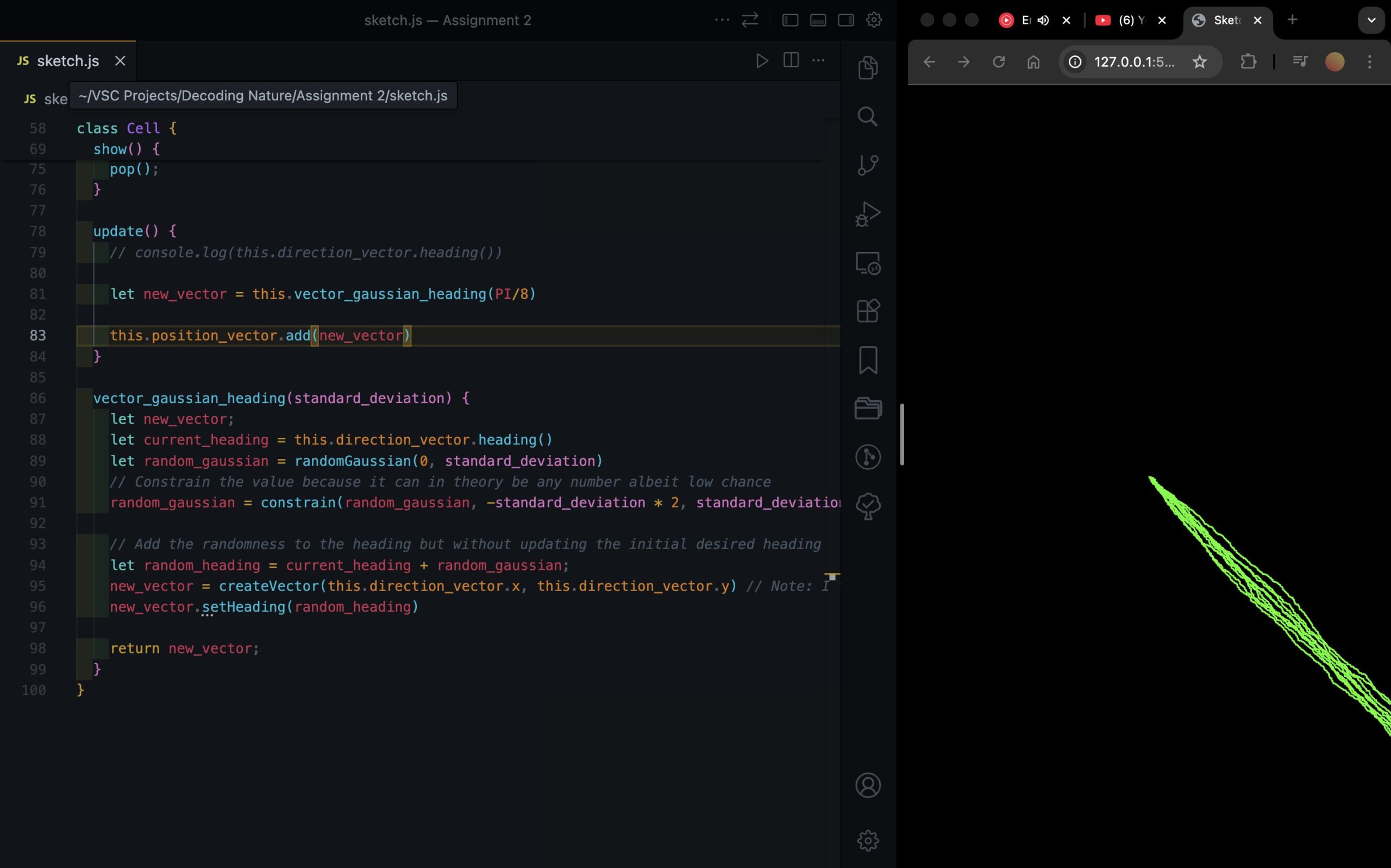
Embedded Sketch

Milestones and Challenges

I started by making particles move toward a goal and then added trails so you could see their paths. Adding turbulence made the movement look more natural and interesting. Creating walls and figuring out how to push particles away smoothly was hard but important for realistic motion. I had to try different force strengths because if the push was too strong, particles got stuck, and if it was too weak, they went through walls. Using a semi-transparent background helped the trails build up visually, and limiting particle speed kept the motion steady.

Reflection and Future Work

This project helped me better understand how multiple forces interact to create complex, emergent movement. Compared to the simpler exercises we did in class, this system feels more full and alive because the forces come from the environment, not just between particles. It was exciting to see invisible forces made visible through the trails the particles leave. In the future, I want to add things like walls you can change with the mouse, more goals for particles to follow, moving obstacles, colors that change based on force, and sliders to adjust settings while the program runs.

Concept

For this assignment, I chose to create a particle system where movers orbit multiple attractors while being affected by three competing forces: gravitational attraction, wind turbulence, and mutual repulsion. I was inspired by how celestial bodies orbit in space but also how flocking birds maintain spacing while moving together. The challenge was to balance these three forces so they create beautiful, flowing patterns rather than chaotic scattering or rigid clustering. Each mover has slightly different mass, giving them unique orbital behaviors – some get pulled strongly into tight orbits while others drift lazily at the edges. The combination of ordered attraction and chaotic turbulence creates movement that feels organic and alive, like watching a cosmic dance that’s constantly evolving but never repeating.

Sketch

Code Highlight

In my implementation, a section of my code that I am proud of is below:

//Wind/turbulence using Perlin noise
 applyWind(time) {
   //perlin noise to create flowing, organic wind
   let noiseVal = noise(this.pos.x * 0.01, this.pos.y * 0.01, time * 0.0001);
   let angle = noiseVal * TWO_PI * 2;
   let wind = createVector(cos(angle), sin(angle));
   wind.mult(WIND_STRENGTH);
   this.applyForce(wind);
 }

This creates the organic turbulence that pushes movers around. Instead of using random() which would make particles jitter randomly, I used 3D Perlin noise (x, y, and time) which gives smooth, flowing forces. By sampling the noise field at the particle’s position and the current time, nearby particles experience similar wind direction, creating swirling currents rather than chaos. The angle conversion means the noise controls which direction the wind blows, creating those beautiful flowing patterns you see in the trails. I’m also proud of this snippet that prevents particle clustering:

//repulsion from another mover
 repel(other) {
   let force = p5.Vector.sub(this.pos, other.pos);
   let distance = force.mag();
   
   //repel if close enough
   if (distance < REPULSION_DISTANCE && distance > 0) {
     let strength = (this.mass * other.mass) / (distance * distance);
     force.setMag(strength);
     this.applyForce(force);
   }
 }

This uses the same inverse-square physics as attraction, but only activates when movers get close. It’s what keeps the particles from all collapsing into a single clump and creates those satisfying spacing patterns in the orbits. It’s a small detail but makes a huge difference in creating visually interesting formations.

Challenges
Force Accumulation Bug
Early in development, I noticed that movers were only responding to one force at a time, even though I was calling applyForce() multiple times per frame. After debugging, I realized the class example’s applyForce() method was replacing acceleration instead of adding to it:

Version from class example:

applyForce(force) {
   this.acc = force.div(this.mass);}

My updated version:

//accumulates forces
applyForce(force) {
  let f = force.copy();
  f.div(this.mass);
  this.acc.add(f); //add to acceleration
}

Reflections and Future Improvements
Through this assignment, I discovered that emergent complexity comes from simple rules interacting. No single force creates the beautiful patterns – it’s the tension between attraction (pulling together), repulsion (pushing apart), and turbulence (stirring things up) that generates the endless variety. My biggest challenge was finding the right balance between these forces. Too many attractions and everything collapsed into the attractors. Too much repulsion and particles scattered. Too much wind and chaos took over. The sweet spot where all three forces balanced created the most interesting patterns. My biggest takeaway is that personality comes from variation. Giving each mover a random mass (between 0.5 and 2) meant they all respond differently to the same forces – heavy particles orbit tightly while light ones drift widely. This variation is what makes the system feel alive rather than mechanical. Below are some ideas I would implement in the future for improvement of what I have currently:

1. 1. Ability to drag attractors to new positions and see how the system responds in real-time.
   2. Make particles bounce off each other with momentum conservation.
   3. Slow motion or fast forward to study patterns at different speeds.
   4. Different colored particles with different masses or charge (attract some, repel others).

With my implementation so far, some features I believe work very well include the Perlin noise wind creating smooth organic turbulence, the speed-based coloring that immediately shows which particles are moving fast, the repulsion preventing unrealistic clustering, and most importantly, the combination of three different forces creating complex emergent behaviors from simple physical rules. The system creates genuinely unpredictable patterns while maintaining a cohesive aesthetic – each session is unique but always visually interesting.

Concept

In class, we mostly looked at one object following one attractor. For this assignment, I wanted to see what happens when multiple attractors and repulsors fight for control over thousands of tiny particles.

• The Magnets: I placed 3 invisible “charges” on the screen. Some pull (Attractors) and some push (Repulsors).

• The “Weavers”: These are hundreds of tiny particles that spawn, trace the invisible lines of force for a short time, and then vanish.

• The Turbulence: To stop the pattern from looking too perfect and mathematical, I added wind using Perlin Noise. This adds a slight wobble to the particles, making the final drawing look like organic flow—like muscle fibersl

• Interaction: Clicking the mouse adds a massive “Disruptor” force (Repulsion) that pushes the flow away from your cursor, carving a hole in the pattern.

Code Highlight

I am particularly proud of the applyBehaviors function. This is the engine that drives the movement. It calculates the “Net Force” for every particle by summing up three different influences: the structural pull of the magnets using vector subtraction, the organic flow of the Perlin noise, and the interactive push of the mouse.

applyBehaviors(magnets) {
    let netForce = createVector(0, 0);

    // A. FORCES FROM MAGNETS
    for (let i = 0; i < magnets.length; i++) {
      let m = magnets[i];
      let force = p5.Vector.sub(m.pos, this.pos);
      let dist = force.mag();
      
      // Avoid extreme forces when very close
      dist = constrain(dist, 10, 100); 
      
      // Physics: Force = Strength / Distance
      force.setMag(m.strength / dist);
      netForce.add(force);
    }

    // B. MOUSE REPULSION (Interaction)
    if (mouseIsPressed) {
      let mousePos = createVector(mouseX, mouseY);
      let mouseForce = p5.Vector.sub(this.pos, mousePos); // Points AWAY
      let dist = mouseForce.mag();
      
      if (dist < 150) {
         mouseForce.setMag(5); // Strong push
         netForce.add(mouseForce);
      }
    }

    // C. TURBULENCE (Perlin Noise)
    // Makes the lines look like wood grain or flowing water
    let n = noise(this.pos.x * 0.005, this.pos.y * 0.005);
    let angle = map(n, 0, 1, 0, TWO_PI);
    let wind = p5.Vector.fromAngle(angle);
    wind.mult(0.5); // Add just a little bit of organic chaos
    netForce.add(wind);

    this.applyForce(netForce);
  }

Milestones & Challenges

I first started experimenting with how to make a magnetic field in p5, so I made a sketch with a bunch of rods that follow the mouse which acts as a magnet. They rods created a nice magnetic field pattern which inspired the final piece.

I learned how to do this from this sketch.

After that, I began playing around with different colors and ended up deciding on this neon purple one with a dark background. Here, the mouse was the magnet, but I noticed that after some time following the mouse, the particles would all be on top of each other and show as one. Because of this, I decided to put multiple attractors, which made no two particles follow the same path.

Reflection & Future Work

This project felt like a significant step up because I was simulating a system of forces rather than just a single interaction. The result looks less like a computer simulation and more like a generative painting.

Future Ideas:

1. Color Mapping: Map the color of the line to the stress (force magnitude) at that point. High-stress areas (near magnets) could be red; low-stress areas could be blue.

2. Moving Magnets: Have the magnets slowly drift around the screen using sine waves, causing the pattern to shift and morph over time.

Concept:

Inspired by the painterly textures of schools of fish avoiding predators like sharks and the concept of “Mutual Attraction” from the Nature of Code, I developed a sketch imitating what you would see if you observed predators and prey in the ocean. My goal was to move away from literal physics simulations and create something that looks – well – cool. The sketch features a shimmering school of prey (teal brushstrokes) and a few large predators (dark purple shadows). The entire system is governed by mutual influence, where every body pulls on every other body, creating a complex, swirling choreography.

In this ecosystem, the movement is defined by a specific hierarchy of forces. The Prey are mutually attracted to one another to create a “schooling” effect, while Predators are naturally drawn toward the prey. To simulate life-like behavior, I flipped the gravitational pull into a strong repulsion whenever a predator gets too close to a prey object, causing the school to scatter in fear. Finally, I added territorial repulsion between the predators themselves; this ensures they don’t clump into a single mass and instead spread out to hunt across the infinite wrapping canvas (more on this later).

Sketch:

Highlight:

I’m particularly proud of how I used Mass to influence the Visual Design. Instead of just drawing a circle, the mass of the object dictates the strokeWeight of the brushstroke, and its velocity dictates the direction and length of the “paint” line:

show() {
  push();
  // Mass determines the thickness of the brush
  strokeWeight(this.mass / 2); 
  
  // Velocity determines the direction and length of the stroke
  let p = this.position;
  let v = this.velocity.copy().mult(4); 
  line(p.x, p.y, p.x + v.x, p.y + v.y);
  pop();
}

Process and Challenges:

I started by creating 100 small “Prey” objects with mutual attraction. This created a beautiful, tight-knit shimmering school.

Then, I introduced “Predators” with higher mass. Initially, they just drifted. I had to implement a Fear rule where the attraction force was multiplied by a negative number if the interaction was between a predator and a prey.

I then experimented with how the creatures should leave the canvas. I settled on Screen Wrapping, as it allowed the painterly trails to feel continuous and infinite, rather than being interrupted by a wall.

A major hurdle was that the predators would eventually find each other and merge into one giant dark smudge. Because they were heavy, their mutual attraction was too strong to break. I solved this by adding a rule that specifically makes predators repel each other while still being attracted to the prey. You can see how they clumped together in this recording:

Reflection:

In the reading from The Computational Beauty of Nature, Gary William Flake discusses reductionism, the idea that systems can be understood by their individual parts. By defining just three simple rules (Attract, Scare, Repel), a complex eco-system emerged on my screen. For future work, I want to explore Oscillation. I would love to make the fish shimmer or vibrate as they move, mimicking the way light reflects off fish scales in deep water. I could also address the clumping problem in the prey which becomes apparent if you hold them together with the mouse for a while. But that’s a fix for another day.

This sketch is a kaleidoscopic illustration of movers and attractors. My main inspiration is a combination of the picture above and a mix of effects I used in one of my motion graphics/VFX projects. I wanted to recreate a sample that captures both feelings at once.

I started this sketch by placing circular attractors as shown in the image.

I wrote code that creates a circular arrangement of attractor points around a center position.

  for (let i = 0; i < numAttractors; i++) {
    let angle = (TWO_PI / numAttractors) * i;
    let x = centerX + cos(angle) * attractorRadius;
    let y = centerY + sin(angle) * attractorRadius;
    attractors.push(new Attractor(x, y, 20));
  }
}

This loop divides the circle into segments, each iteration multiplies by i to get the angle for that specific attractor. For x and y positions, I use polar-to-cartesian coordinate conversion as shown in the code.

Then I added movers and I applied the forces to the movers such that their position is affected by the attractors.

For this effect I take inspiration from this code.

So basically, the kaleidoscope effect happens because every single object gets drawn (numAttractors) times instead of just once. The trick is that before drawing each copy, the code rotates the entire coordinate system around the center of the canvas by increments of 60 degrees (since 360 deg ÷ 6 = 60 deg). It does this by moving the origin to the canvas center, rotating, then moving it back, and finally drawing the object at its actual position. But because the whole coordinate system has been rotated, what you actually see is the object appearing in six different spots arranged symmetrically around the center, like looking through a kaleidoscope. The cool part is that the physics simulation itself, only happens once for each object, but visually you see six reflections of everything. So when a mover orbits an attractor, all six of its mirror images orbit simultaneously.

For example, the number of movers in this sketch is 1, but it gets reflected 5 times

Here’s the code responsible for the kaliedoscope effect

for (let i = 0; i < symmetryFold; i++) {
  push();
  translate(width / 2, height / 2);      // move origin to center
  rotate((TWO_PI / symmetryFold) * i);   // rotate by incremental angle
  translate(-width / 2, -height / 2);    // move origin back
  circle(this.position.x, this.position.y, size);  // draw at original position
  pop();
}

I then made some really interesting changes here that make the pattern way more complex and controlled. I added this clever touch of four “corner attractors” placed at each corner of the canvas with higher mass , which act like gravitational anchors that influence the overall flow and create an effect of repulsion. I also added a visibility toggle (showAttractorsRepeller) so I can hide the attractors if I just want to see the trails. Speaking of trails, I changed the background to fade super slowly with background(0, 1) instead of clearing completely each frame, which creates these motion trails that build up over time. And finally, I made the movers wrap around the screen edges, if one goes off the right side it reappears on the left, which keeps the pattern continuous and prevents movers from escaping the canvas entirely.

Then I hit the jackpot. By changing one of the corner attractors mass, I create really interesting kaleidoscopic effects as shown in the gif below

Then by playing with the number of attractors I achieve really compelling visual effects like this

Sketch

To get the most out of this sketch, please manipulate the parameters I indicated at the top of the code. There’s something so super satisfying with watching those patterns slowly get created.

  show() {
    fill(255, 100, 100);
    noStroke();
    
    // draw attractor with radial symmetry
    for (let i = 0; i < symmetryFold; i++) {
      push();
      translate(width / 2, height / 2);
      rotate((TWO_PI / symmetryFold) * i);
      translate(-width / 2, -height / 2);
      circle(this.position.x, this.position.y, this.mass * 2);
      pop();
    }
  }
}

Concept

For this week’s assignment I wanted to recreate one of the most beautiful motions in nature, shooting stars. My idea was to have the stars fall from the top but be affected by the planets gravity which changes their direction. I also decided to add a path (line) behind the shooting starts which slowly filles up the screen and creates this beautiful drawing of all the paths the stars took. The users can also click on the screen to move the planets around and thus create completely unique paths every time.

Process

First order of business was to create the star filled background and to add planets. This is also when I added the click to add planets function so I wouldn’t have to deal with it later.

After this was done it was time to get started on adding shooting stars. I decided to also give them a trail so they would actually look nicer while “falling” and wouldn’t just be a ball passing by.

This is done by first saving the last position of the star as the first one in the array:

// save tail
this.tail.unshift(this.pos.copy());
if (this.tail.length > this.tailMax) this.tail.pop();

After which we draw the tail on the last position of the star with this:

draw() {
  // Tail
  for (let i = 0; i < this.tail.length - 1; i++) {
    let a = map(i, 0, this.tail.length - 1, 220, 0);
    let w = map(i, 0, this.tail.length - 1, 10, 1);
    stroke(255, 255, 255, a);
    strokeWeight(w);
    line(this.tail[i].x, this.tail[i].y, this.tail[i + 1].x, this.tail[i + 1].y);
  }

And now we have a tail following the star. I also added the “this.tail.pop()” to make sure the last position in the array (not the starts last position, technically the “first” ones) is deleted to keep the array shorter. And now we had shooting stars in the sketch.

But I felt like something was missing so I added the lines that are left behind the start so add a nice trail like drawing to the experience. To do this I decided to use createGraphics to keep it cleaner and more organized and to make sure the paths will always be visible. Using createGraphics also allowed the trail drawing to persist independently of the main animation loop, which clears each frame. This separation made it possible to accumulate motion into a lasting visual pattern.

pathLayer = createGraphics(width, height);
pathLayer.clear(); // transparent at the start

let prev = s.pos.copy();
s.update();
// draw path
pathLayer.stroke(255, 35);
pathLayer.strokeWeight(1.2);
pathLayer.line(prev.x, prev.y, s.pos.x, s.pos.y);
s.draw();

The prev stores where the star was before updating and the update moves the star. Then we use .line to create the path which when run every frame creates the path that we see in the final product.

Code Highlight

Even though my proudest part of code is the path layer one where I create a path behind the shooting stars, since I went over that part of the code I will explain my second proudest.

function solarWind(x, y) {
  let a = noise(x * 0.01, y * 0.01, frameCount * 0.01) * TWO_PI * 2;
  return p5.Vector.fromAngle(a).mult(WIND);
}

This, even though simple code I believe adds a nice touch to the overall feel and vibe of the sketch. Rather than applying random turbulence, I used Perlin noise to generate a smooth directional field across space. The noise value is converted into an angle and then into a vector, producing gentle, continuous variations in star motion. This force adds complexity without visual chaos, allowing trajectories to subtly diverge while still being primarily governed by planetary gravity.

Future Improvements

I am incredibly proud of how the final code turned out, but if I was to change anything in the future I would probably play with the color of the path that follows the shooting stars and or maybe it’s thickness. I would also explore the possibility of adding more planet options or maybe even planet star collision system.

This sketch went through more versions than I expected. What I’m submitting now is not where I started at all. The process was mostly about learning when to stop adding, when to remove, and when to trust small decisions like color and speed instead of big visual tricks.

Rather than drawing literal objects, I wanted to treat the canvas like a sky that slowly paints itself. The goal was to get something that feels alive and emotional through motion alone, without relying on obvious symbols.

Concept

The sketch is made up of many moving walkers that act like brush strokes. Each one follows a smooth flow field, creating large swirling currents across the canvas. Small warm dots are scattered in the space. They are intentionally subtle and not meant to be read as stars directly. Instead, they influence the motion by creating gentle swirling forces around them.

Movement is more important than form here. The drawing builds up slowly over time as strokes overlap, fade, and accumulate. I wanted the sketch to feel closer to painting than animation.

Inspiration

The main inspiration was The Starry Night by Van Gogh, but specifically the energy of the sky, not the imagery. I was drawn to how the sky feels restless, emotional, and alive. I wanted to translate that feeling into motion and color, without copying shapes or composition directly.

I was also thinking about painterly mark-making and how repetition and gesture can build texture and depth.

Milestones and process

This project was very much a trial-and-error process, and each milestone came from something not working visually.

Milestone 1: Realizing movement alone wasn’t enough
The first versions technically worked but looked bad. The motion was chaotic and noisy, and everything competed for attention. Even though there was a lot happening, nothing felt intentional. This was when I realized that having a system is not the same as having a composition.

Milestone 2: Struggling hard with color
Color was the longest and most frustrating part. Early versions were way too neon and saturated. They felt more like a screensaver than a painting. I kept tweaking values and nothing clicked until I made a decision to restrict the palette almost entirely to deep blues. Warm tones were allowed only in very small amounts. That shift changed everything. Once the palette was limited, the sketch finally started to feel grounded and cohesive.

Milestone 3: Changing how forces work
At first, I used direct attraction, which caused clustering and visual clutter. Everything kept collapsing into points. Switching to a tangential force that makes walkers swirl around dots instead of moving toward them was a turning point. This single change transformed the sketch from messy to controlled and gave the motion a calm, circular rhythm.

Milestone 4: Removing visual elements
This was a big one. I tried adding glowing stars, silhouettes, and other focal points, but they kept overpowering the motion. Removing them made the piece stronger. Each time I deleted something, the sketch improved. This taught me that generative work benefits a lot from editing and restraint.

Milestone 5: Slowing everything down
The final milestone was reducing speed and force. Earlier versions moved too fast and felt anxious. Slowing the walkers and letting the trails accumulate over time made the sketch feel more meditative and painterly. This is when it stopped feeling like an experiment and started feeling like an artwork.

Code highlight

This section of the code was crucial to reaching the final behavior. Instead of pulling walkers inward, it pushes them sideways so they orbit and swirl:

That small change completely reshaped the motion and helped the sketch feel intentional rather than chaotic.

Coded embedded 

Reflection and future work

This project taught me how important restraint is in generative art. The sketch became stronger every time I simplified it. Color, speed, and force mattered far more than adding new visual elements.

In the future, I want to explore:

• Using fewer walkers to increase negative space

• Creating print-focused versions with stronger contrast

• Letting the flow field change slowly over time to create different emotional phases

So far honestly I am so so proud of myself for creating this and I loved it

Concept

For this assignment, I built a night-sky inspired sketch using attractors and movers. In class, we used the attractor/mover system to show motion and forces, and I kept thinking: if attractors “pull” and movers “orbit,” that feels a lot like stars/planets. So my concept became a stylized sky at night, with glowing star bodies and drifting trails.

To add a personal twist, I placed my initials (ABJ) in the center as a constellation-like pattern made from many tiny attractor/mover pairs. The initials stay readable, but still wobble and respond to the mouse so they feel “alive.” Also to be honest this assignment wasn’t the easiest for me and isn’t my favorite, but it’s the best I can do so far with attractors and movers and I learned a lot through iteration 🙂

Inspiration

My main inspiration is simply the sky at night: glowing points, soft halos, and a sense of motion even when things are calm. I didn’t copy a specific image but I had the starry night in mind by Van Gogh. 

Sketch

How the code is organized

The code is organized  sections so the behavior stays understandable even as the sketch becomes more complex. I use two main classes: Attractor and Moverwhere attractors apply a gravitational-style force and movers respond with velocity and acceleration. Several helper functions control additional forces: repelFromMouse() pushes movers away from the cursor to add interactivity, applyTurbulence() introduces Perlin-noise-based motion so the movement feels organic instead of mechanical, and springTo() pulls movers back toward a target position. Scene-building functions like addMainOrbitPairs(), addEdgeOrbitPairs(), and addInitialsABJ() handle different visual systems in the sketch, separating setup from animation logic.

Code highlight I’m proud of

The part I’m most proud of is how I built the ABJ initials using point generators + tiny attractor/mover pairs. Each point of each letter becomes a mini “star” that’s pulled into place, wiggles with turbulence, repels from the mouse, and springs back to stay readable:

// Build ABJ using many tiny attractor+mover pairs.
// Each letter point is a fixed attractor with a mover that wiggles around it.
function addInitialsABJ() {
  let cx = 200, cy = 200;
  let letterW = 32, letterH = 48, spacing = 38;

  let oxA = cx - spacing - letterW / 2;
  let oxB = cx - letterW / 2;
  let oxJ = cx + spacing - letterW / 2;
  let oy = cy - letterH / 2;

  let aPts = letterAPoints(0, 0);
  let bPts = letterBPoints(0, 0);
  let jPts = letterJPoints(0, 0);

  for (let [lx, ly] of aPts) {
    let ax = oxA + lx;
    let ay = oy + (letterH - ly); // A is flipped vertically
    initialsPairs.push({
      attractor: new Attractor(ax, ay, 40),
      mover: new Mover(ax + random(-4, 4), ay + random(-4, 4), 1.2, 2, 0.05, 0.05),
    });
  }

  for (let [lx, ly] of bPts) {
    let ax = oxB + lx;
    let ay = oy + ly;
    initialsPairs.push({
      attractor: new Attractor(ax, ay, 40),
      mover: new Mover(ax + random(-4, 4), ay + random(-4, 4), 1.2, 2, 0.05, 0.05),
    });
  }

  for (let [lx, ly] of jPts) {
    let ax = oxJ + lx;
    let ay = oy + ly;
    initialsPairs.push({
      attractor: new Attractor(ax, ay, 40),
      mover: new Mover(ax + random(-4, 4), ay + random(-4, 4), 1.2, 2, 0.05, 0.05),
    });
  }
}

// In draw(): update ABJ using multiple forces so it moves but stays readable.
for (let p of initialsPairs) {
  p.attractor.attract(p.mover);          // pulls toward letter point
  p.mover.applyTurbulence(t * 0.3);      // gentle wiggle
  repelFromMouse(p.mover, 0.6);          // weaker mouse repulsion
  springTo(p.mover, p.attractor.pos, 0.018); // snaps back to letter shape
  p.mover.update();
}

Milestones + challenges

• My first idea was using an image background (like a starry-night painting) and layering moving stars on top of it. I got it working, but visually it felt more like “decorating an image” than building a system, so I scrapped that direction. 
• I switched to a fully generated background with glows and stars, and started focusing on the attractor/mover motion as the main design elements

• Adding the ABJ initials was the biggest step: it made the sketch feel personal and gave me a focal point.

• Challenge: The hardest part was balancing turbulence. Too little and everything looked static; too much and the motion became chaotic and the initials stopped reading as letters. I had to iterate on turbulence strength and also add a spring force so the ABJ points could move while still returning to a clean letter structure.

Reflection + future improvements

If I continued this project, I would improve the “sky” depth by adding multiple layers of stars that move at different speeds (parallax). I’d also experiment with making the attractors slowly drift so the whole constellation system evolves over time. Also, in this assignment you get the nature of the sky, but it doesn’t feel natural, so that’s something that I need to keep in mind.

Concept

This project explores how small particles in nature respond to invisible forces in their environment. I was inspired by drifting pollen, spores, and algae suspended in water. These natural elements do not move randomly. They respond to forces such as gravity, air currents, and nearby bodies.

Using the attractor and mover structure introduced in class, I reinterpreted the system as an ecological field. The attractors function as environmental centers of influence. The movers behave like pollen particles that continuously respond to these forces. Instead of presenting a physics demonstration, the system is used to generate an evolving visual pattern.

The visual accumulation of trails transforms the physical simulation into a generative design.

Code Highlight

One section I am particularly proud of is the gravitational force calculation inside the attractor. This formula controls how each particle responds to distance and mass, and it was important to balance it so that movement felt stable but still dynamic.

This part connects directly to the force and acceleration principles explored in class.

let force = p5.Vector.sub(this.pos, mover.pos);

let distance = constrain(force.mag(), 20, 250);
force.normalize();

let strength = (this.G * this.mass * mover.mass) / (distance * distance);
force.mult(strength);

return force;

Code

Milestones and Challenges